The Porcelain Tower of Nanjing. The original was Destroyed in the 19th century but the replica has the same size and octagonal shape. If the diameter of the base is 30m and the height is 79m, assuming the same cross-section throughout, what is the volume?

Scroll down for my solution

.

.

.

.

.

.

.

.

.

.

.

.

Solution

The formula for the area of a regular octagon is 2*(1 + sqrt(2))*s² where a is the length of each of the 8 sides of the octagon. However, since we do not know s initially, we may use the following diagram:

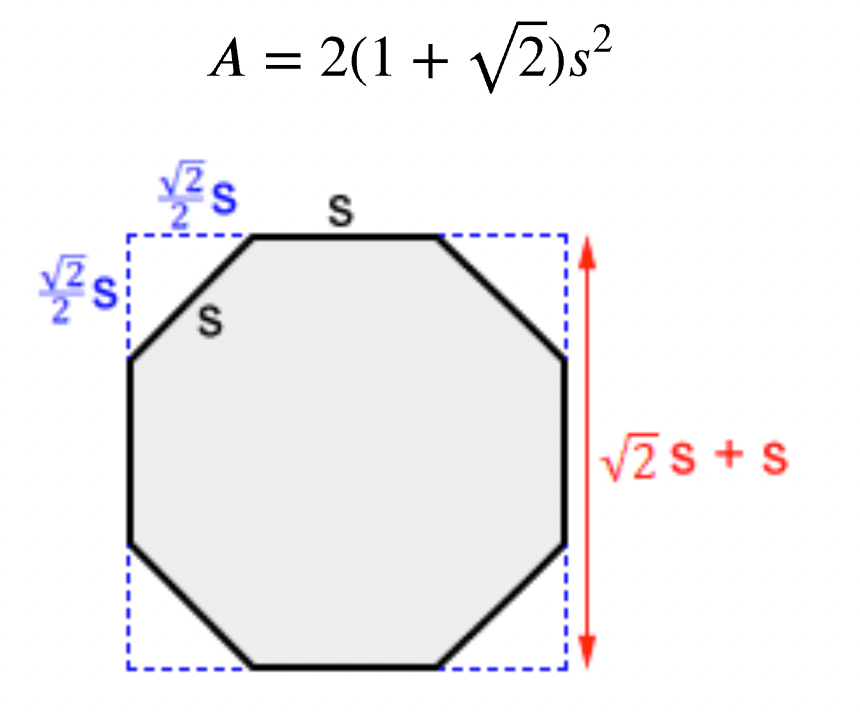
From the information given, we know the diameter is 30m. This is equal to (1 + sqrt(2))*s in the diagram above. Therefore, s = 30 / (1 + sqrt(2)) = 12.43 and so the area is
2*(1 + sqrt(2))*(12.43)² = 746 m²

We then multiply by the height of 79m to get the volume V = 746*79 = 59,000 m³