Views for days from the Maokong Gondola in Taipei. My first visit to Taiwan and I’m loving it so far! The gondola is split into 3 parts, with the first going from 24.1m to 95.5m and across 1297m, the second increasing in height to 264.3m and across a further 1628m, and the third increasing to a final height of 299.3m and across a further 1108m. At maximum speed the journey takes 17 minutes – how fast can it travel?

Scroll down for my solution

.

.

.

.

.

.

.

.

.

.

.

.

Solution

Here is a diagram of the gondola route (from Bermuda Rover):

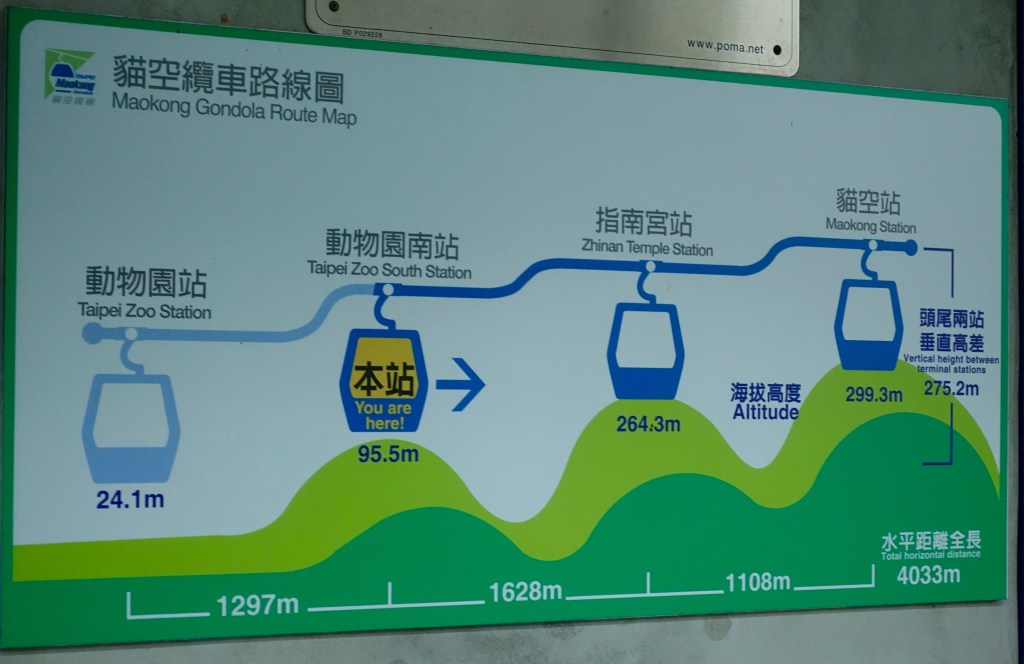
Assuming each line is triangle for simplicity, we have the following:

Part 1: height 71.4m, length 1297m, so by Pythagoras the hypotenuse (distance travelled) is 1299m.

Part 2: height 168.8m, length 1628m, so by Pythagoras the hypotenuse (distance travelled) is 1636.7m.

Part 3: height 35m, length 1108m, so by Pythagoras the hypotenuse (distance travelled) is 1108.6m.

Distance = 1299 + 1636.7 + 1108.6 = 4044.3m
Time = 17 minutes or 17*60 = 1020 seconds.

Speed = 4 m/s