I loved exploring the ‘lanes’ of Melbourne and their incredible street art, which naturally led me to come up with a maths problem (thanks brain). If we simplify the map and take it to be a 5×5 grid, starting from the bottom left corner, and only being able to move right or up each time, how many different paths are there that end at the top right corner?

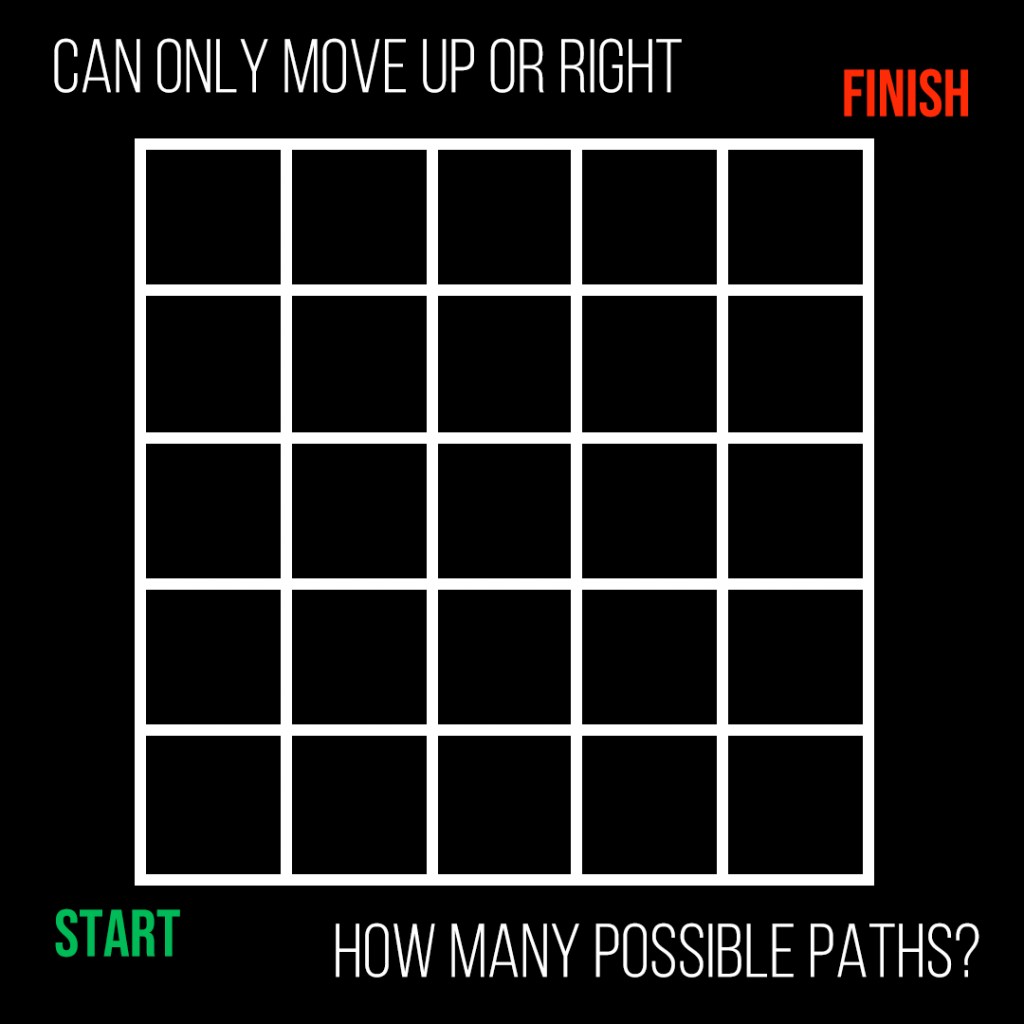
Scroll down for the solution!

.

.

.

.

.

.

.

.

.

.

.

.

Solution

To move from the ‘start’ to the ‘finish’ you need to take 5 horizontal steps and 5 vertical steps in any order. Since the direction of each is fixed (ie. right and up) the only choice you have is whether to move horizontally or vertically each time. Given the total number of steps will be 10 – regardless of the path you choose – and there must be 5 of each type, once you have decided at which steps to move horizontally (for example), the others are all fixed. Therefore, you have to decide where to place the 5 horizontal steps out of a possible choice of 10 locations. Each such combination will give rise to a different path, so the final answer is 10 choose 5 – exactly how we define the number of ways to place 5 objects in 10 possible positions.

10 choose 5 = 10! / (5! * 5!) = 10*9*8*7*6 / 5*4*3*2*1 = 252.

There are 252 possible paths across the 5×5 grid of ‘lanes’.