Jakub Michalski

The Monty Hall problem first graced the world of mathematics in 1990 with a letter sent to Marilyn vos Savant, an American magazine columnist, who at the time was listed in the Guinness Book of World Records as having the highest recorded IQ of anyone alive: 

Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice? 

This riddle is based on the show “Let’s Make a Deal” whose host was Monty Hall – which is where the name of the problem comes from. 

Most people intuitively answer that it doesn’t matter, both doors have equal probability (to be exact, in one study only 12% of people decided to switch). However, von Savant concluded that the contestant should always switch to have the highest chance of winning. After publishing the answer and explanation in her column, she received thousands of letters whose authors (many of which were educated people with PhDs) tried to prove her wrong. However, she was, in fact, right. 

To prove this, you can simply draw a table with all of the cases, and you’ll see that when you switch the door, your chance of winning is 2/3 and when you stay it’s 1/3: 

Contestant’s initial choice	Prize door	Don’t switch	Switch
1	1	Win	Lose
1	2	Lose	Win
1	3	Lose	Win
2	1	Lose	Win
2	2	Win	Lose
2	3	Lose	Win
3	1	Lose	Win
3	2	Lose	Win
3	3	Win	Lose
		3 Wins	6 Wins

But this is not really an interesting solution, because it doesn’t help us to grasp what exactly is going on. 

To build our intuition on this problem, let’s start with something slightly different: Suppose you want to pick the ace of spades from a deck of cards. First, you draw one card. You have a 1/52 chance of having the ace of spades in your hand. Now, ask your friend to discard from the deck 50 cards that are not the ace of spades. Should you now stay with your initial card, or choose the one remaining card left in the deck? Here, it seems more obvious that you have a bigger chance of succeeding if you change your original choice. 

Now, back to our original question. Let’s number the doors 1, 2, 3. Initially each door has 1/3 chance of hiding a car behind it and 2/3 of hiding a goat. Contestant picks door number 1. Let’s group the doors: Group A consists only of the door number 1, and group B includes doors 2 and 3. The probability of the car being in group A is 1/3, and probability for group B is 2/3 (where 1/3 comes from each door): 

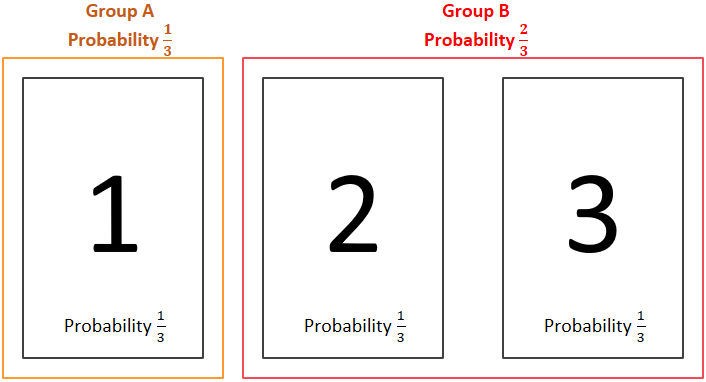
Now, the host opens door number 3. The probability of the car being in group B is still 2/3, but now in this group you can choose only door 2. So, the probability of winning for door 1 is 1/3, and for door 2 is 2/3: 

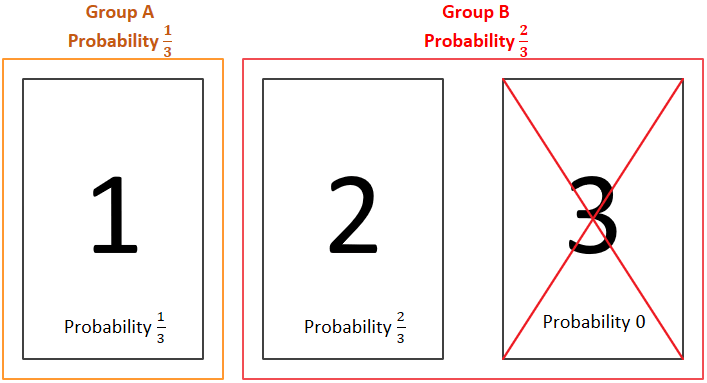
So why do so many people get this problem wrong? After some research and surveying of family/friends, it seems it is probably a sum of a few different effects:  

• When thinking about probabilities people tend to assume that the analysed events are completely random and independent of each other, so they have equal probabilities. In this case they can simply divide the number of winning outcomes by the total number of outcomes. For example, the probability of obtaining tails from coin throw is [Equation] – the number of “winning” outcomes (1) divided by the number of total outcomes (2). In the Monty Hall problem these assumptions are wrong because the choice of doors by the host is not completely random – actually, if the contestant chooses the wrong door it is deterministic. If the car is behind door no. 2 and contestant chooses no. 1 the host has to open door no. 3 – he cannot open door no. 1 because it was already chosen by the participant, and he cannot open door no. 2 because he would reveal were the car is. 

• People always give bigger value to something they have already chosen, what they already own (“the endowment effect”), and favour the current state of the system (“status quo bias”), so they do not want to change their choice to different door. 

• People prefer to make errors by not taking an action than by taking a wrong action (the errors of omission vs the errors of commission), so they prefer to not change their choice and lose than to change doors and lose. 

Ultimately, this problem teaches us that even though intuition is very important for a mathematician, we shouldn’t trust in it completely and that the “proof by intuition” is not enough. Moreover, the story of van Savant shows us that before you reason with somebody, listen carefully to what they’re saying and make sure that you understand their argument. 

If you are interested in probability and paradoxes, check out my two other articles – about probability models and how can they mislead us, and the Bertrand paradox.