Wilf Offord
Cardinal
Our first kind of infinity comes up when we try to work out the answer to the question ‘how many?’ For instance, if we ask how many positive whole numbers there are below 3, the answer is ‘2’. But what about if we ask how many whole numbers there are in total? What about all rational numbers? Not surprisingly, we get the answer ‘infinity’. But what may be surprising is that we can make sense of saying one of this kind of infinity is ‘bigger’ than another! In fact, there are infinitely many of this kind of infinity – the first few are represented by the Hebrew letter א, Aleph, as shown below.

Oridinal
A second kind of infinity comes up when we want to work out the place of something in a sequence. We use ordinals like ‘first’, ‘second’ and so-on to describe this, but now imagine we have an infinite row of objects. It turns out there’s a way to keep ‘counting past infinity’, and talk about the ‘infinity-eth’ place. For this we use transfinite ordinals, the first of which is written as ω, the Greek letter omega. Unlike cardinal infinity, however, it makes sense to talk about the ‘infinity-plus-one-th’ place, so we get that ω is not the same as ω+1! Just like cardinal infinity, there are infinitely many ordinal infinities too, the first few of which are represented below.
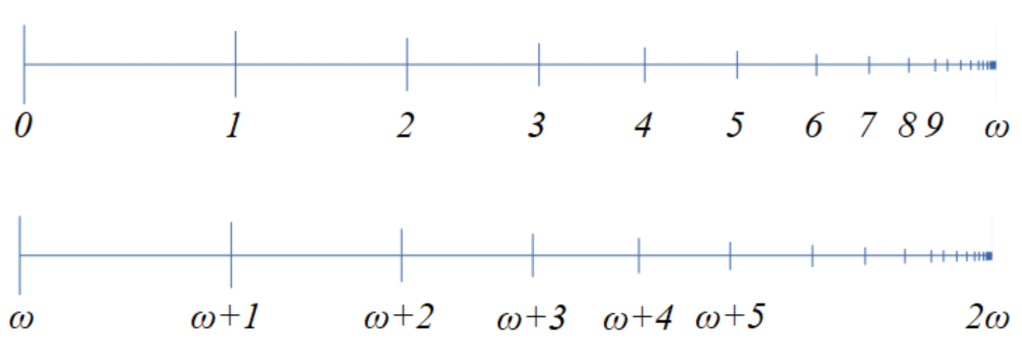
Infinite Series
Here’s a third way mathematicians use infinity: when we want to somehow add up ‘infinitely many numbers’, what do we actually mean by this? Well, we mean that as we keep adding more and more terms, the total gets closer and closer to some ‘limit’. You can see this illustrated in the picture below: we add a quarter, then a quarter of a quarter and so on until we get the area shaded in purple. If you look closely at the white squares left over, you’ll notice they come as two identical copies of the purple sequence – so the infinite series sums up to 1/3 of the original square!

Geometric
We know from geometry that any two non-parallel lines meet in a unique point, but you might wonder if there’s a way of looking at things that allows us say the same for parallel ones. It turns out there is! And this is where we get our fourth kind of infinity. In a field called Projective Geometry, it makes perfect sense to say that two parallel lines actually ‘meet at infinity’ just like in the picture below. When we add in these special ‘points at infinity’, it makes our geometry work much more smoothly in certain contexts.

Riemann Sphere
Finally we have our fifth kind of infinity, the Riemann Sphere. This one will make sense if you’ve ever heard of complex numbers; essentially we make a ‘2D Plane’ of numbers by adding in a number called ‘i’, which is defined to be the square root of -1. But in the realm of complex analysis we can go further: imagine taking our 2D plane, centred at 0, and somehow stretching out the corners into a sphere. Where they meet at the north pole, we add in a final point called ‘∞’. This way we get the Riemann Sphere, pictured below – and this lets us make sense of certain things like saying 1/0=∞. But this is only true in this specialised context – don’t go writing this in maths class!


Before I even read the article, just hearing the question “what types of infinity appear in mathematics?”, this is the list I came up with:
– Ordinals
– Cardinals
– Limit to infinity
– Surreals / non-Archimedean rings
– Hyperreals / non-standard analysis
– Affinely extended real numbers
– Projectively extended real numbers / Riemann sphere / one-point compactification of R^n
– The “line at infinity” in projective geometry / homogenous coordinates
LikeLiked by 1 person
I think Ω is the biggest infinite ordinal.
There are also N⁰,N¹,N²,Nω and Nε.
LikeLike
[…] Testing for Divisibility of ANY Number The Finite Calculus: Part I Differentiation 5 Types of Infinity […]
LikeLike