Chenying Liu

In part 1 we learned Tom’s strategy for trying to catch Jerry, so now let’s here how the mouse plans to escape…

Jerry’s Strategy

Little Jerry, knowing nothing about Tom’s plan, also shows superior intelligence. He decides no matter where Tom is he will run in the direction perpendicular to the radius he is currently on, in the direction opposite to Tom’s current location. Let’s look at an example in the diagram below. Jerry’s location is given by M₁ and Tom’s by C₁. According to Jerry’s strategy, he will run to the upper part of the circle (away from Tom) and make his path perpendicular to OM₁ (the radius Jerry started on).

After running for time period t₁, Jerry arrives at the new position M₂. As long as M₂ hasn’t reached the edge of the stadium, Tom will not have been able to catch Jerry. Here’s why…

As Jerry’s path M₁M₂ is perpendicular to OM₁ and away from Tom’s initial position C₁, angle C₁M₁M₂ is obtuse (greater than 90 degrees). We know that the shortest path for Tom to reach Jerry is the straight line C₁M₂. According to the Cosine Law and the fact that cos(C₁M₁M₂) ≤ 0 (since cos is negative for angles between 90 and 180 degrees), we have: 

Thus, it’s clear that C₁M₂ > M₁M₂. Because both Tom and Jerry move at the same speed, Tom cannot cover a longer distance (C₁M₂) than Jerry (M₁M₂) during the same time period. 

So what happens next? When Jerry is at M₂, Tom will be at some point C₂, which is between C₁ and M₂. What should Jerry do? Again, according to his strategy, he will run away from Tom making his path perpendicular to OM₂.

After time period t₂, Jerry is at some new point M₃. Once again, the quickest way for Tom to reach M₃ is to go in a straight line to that point. However, because of the same reason we demonstrated above, we have C₂M₃ > M₂M₃ and so Tom fails to catch Jerry again. Jerry can now continue to move in this way for as many steps as he wishes to continue to stay out of reach of Tom… However, the condition for this to succeed is that Jerry should never reach the edge of the stadium at any step or Tom may catch him. So, the question now becomes how can Jerry meet this condition?

After thinking for a while, Jerry comes up with the following idea. If we take t to be a very small time period, then Jerry chooses t₁ = Δt, t₂ = Δt/2, t₃ = Δt/3, … , t_n-1 = Δt/(n-1), t_n = Δt/n, … and so on for each of his steps. We now want to know here Jerry will be after n such steps, so let’s calculate his distance to the centre. Suppose that initially Jerry is at point M₁ and call the distance from the centre O to M₁, OM₁ = r₀. 

At Step 2 in Jerry’s strategy, Jerry is at point M₂ and so to calculate his distance from the centre we need to calculate the length of OM₂. We already know that M₁M₂ is perpendicular to OM₁ so the square length of OM₂ can be obtained by Pythagoras’ theorem:

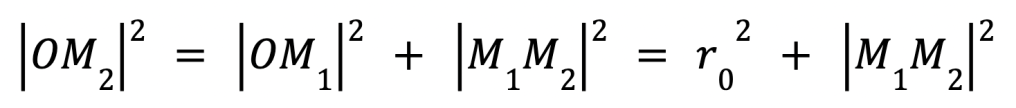
In the third step, Jerry is at point M₃. We know the length of OM₂ from the last step and M₂M₃ is perpendicular to OM₂. Again using Pythagoras’ theorem, (OM₃)² = (OM₂)² + (M₂M₃)². Substituting the value of OM₂ from above, we have the square length of OM₃:

Can you spot the pattern? If we continue in the same way for each of the steps, the square length of (OM_n)² at Step n will be (OM_n)² = (OM_n-1)² + (M_n-1M_n)² and substituting in the formula from the earlier steps we get: 

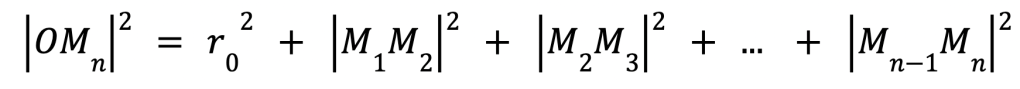
We now have a formula for Jerry’s distance from the centre at step n in terms of the distances M₁M₂, M₂M₃, … , and M_n-1M_n. If we consider Jerry’s speed v and his running time for each step, we can also compute these distances using speed = distance/time. Recall that Jerry has already chosen the time for each step as: 

Step 1: t₁ = Δt; Step 2: t₂ = Δt/2; Step 3: t₃ = Δt/3; … ; Step (n-1): t_n-1 = Δt/(n-1); Step n: t_n = Δt/n, where Δt is some small time period which we will worry about later.

Then the formula distance = speed x time gives

Substituting these values  into the equation for OM_n, we get

by factoring out the v and t terms. 

We could try to calculate a formula for the sum 1 + 1/2² + 1/3² + … + 1/(n – 1)² but we can save ourselves considerable work by instead estimating the value. 

For each term in the sum, we use an inequality to set up the estimation. Now, for any fraction, keeping the numerator unchanged and decreasing the denominator will make the number smaller. For instance, 1/2² = 1/(2*2) < 1/(1*2). Similarly, we can have 1/(n-1)² = 1/(n-1)(n-1) < 1/(n-2)(n-1).

Thus, we can estimate the value of 1 + 1/2² + 1/3² + … + 1/(n – 1)² by

The new sum is ‘better’ than the previous one because it can be calculated much more easily. We first note that the fraction 1/(n-2)(n-1) can be decomposed into: 1/(n-2)(n-1) = 1/(n-2) – 1/(n-1).

Replacing each component of the sum in a similar way, we have:

with all other terms cancelling out. Comparing the two sums, we obtain the estimation as

Therefore we have 

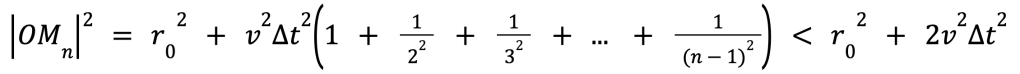
If we call the radius of the stadium r, then to avoid reaching the edge, Jerry always requires (OM_n)²  < r² no matter how large n is (ie. how many steps forward in time he goes). Looking back at the expression for (OM_n)² above, we have 3 variables r₀, v, and t. Jerry’s initial distance to the centre, r₀, is randomly decided. His speed, v, is a fixed value which is the same as Tom’s and decided by the referee of the Endgame. Only the small time period Δt can be controlled by Jerry by how often he changes his direction. This is in fact the key point: can we choose a small enough Δt to make r₀² + 2v²Δt² < r²? If so, then Jerry’s distance from the centre at step n will always be less than the radius of the stadium and he will never be caught.

Fortunately, we can just rearrange the expression above to get

and then Jerry will never hit the edge of the stadium. Jerry is going to make a successful escape! 

There is one final question for us to consider: for how long will Jerry be running? Whilst we have shown that it is possible for him to remain ahead of Tom and away from the edge of the stadium, we need to check for how long he is able to use this strategy. Let’s do another (final) calculation. 

In Step 1, Jerry has chosen time t₁ to be Δt, a short time period meeting the inequality above. In Step 2, Jerry will use time t₂ which equals to Δt/2. Thus the total time he uses after Step 2 is t₁ + t₂ = Δt + t₂. The time period he spends on Step 3 is t₃ = Δt/3 and the total time adds up to t₁ + t₂ + t₃ = Δt + t₂ + t₃ etc.

Therefore, the whole time t after Step n is just equal to the total time of each step added together, and so is given by:

t = t₁ + t₂ + t₃ + … + t_n-1 = Δt + Δt/2 + Δt/3 + … + Δt/(n – 1)

or more succintly

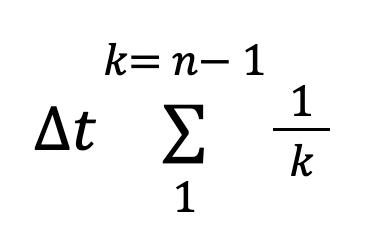
If you’ve heard of the famous harmonic series, you’ll know this is a divergent infinite series. Thus, in our sum, as n approaches infinity, the total will also tend to infinity. And although Δt can be extremely small, it remains non-zero and thus, multiplying the sum by Δt also gives infinity, which means the running time for Jerry can be extended indefinitely! 

So what does this mean for the rules of our Endgame? Well, first we might want to set a time limit or it seems it may never end. But, provided he follows the strategy set out in this article, Jerry will always remain out of Tom’s grasp and be crowned the champion! Some things never change…