Caitlin Moeran – Student Winner of the 2021 Teddy Rocks Maths Essay Competition

Mathematicians love to tell us their work is beautiful. This is not personal vanity, maths really is beautiful. The symmetry, interrelationships, and sense of completion that a problem can give us are what makes maths so attractive to me and others. I would also argue however, that the beautiful is mathematical.

In my history of art class we were studying Hokusai’s ‘The Great Wave off Kanagawa’. It is an extremely well-known piece and it is relatively common knowledge that it utilises the golden ratio (roughly 1: (1+√5)/2). The golden ratio is everywhere in art because our brains find it aesthetically pleasing, and because, once aware of it, artists find it easy to spot and recreate. Perhaps more interesting is the uncanny resemblance of the forms in ‘The Great Wave…’ to the Mandelbrot set. The sea foam furls outwards in groups of what look like claws, and this bulbous mass is mirrored by the clouds in the background. It could be coincidence that the continuous curls and forms of the Mandelbrot set are also found in Hokusai’s work, but when you see the repeating similarities it seems unlikely. The Mandelbrot set is a fractal, something that repeats itself over and over at a smaller scale each time, and is used to model waves (specifically the break/lip of a wave) in science. Hokusai was somehow aware of the mathematical structure of a wave, and from this was able to recreate it and design a hugely successful print.

Fractals also appear in other, very different, works of art. Jackson Pollock is famous for his abstract ‘poured paintings’, where paint is splashed, burst, dripped, and dribbled onto the canvas. The pieces are active and absorbing, and so far have stood the test of time (the first ‘drip painting’ was made in 1947, and is still well known and talked about). Although there are no natural curves, nor recognisable forms, there is an organic, animate nature to these pieces. Like all good modern art it provokes an emotional response in us, we just cannot explain why. Except perhaps maths can. Pollock’s work functions as a fractal (i.e. it repeats itself in ever decreasing proportions). We don’t just find fractals in waves, we find them everywhere in nature, from the spread of electricity to the clustering of a Romanesco broccoli. And this structure cannot have been chosen consciously by Pollock. The term fractal was only coined in 1975, his first painting of this sort was made in 1947, 22 years before. Intuitively, in his self-described haze of painting, Pollock was crafting mathematical masterpieces.

The artist with the most impressive instinctive appreciation of mathematics in art was Van Gogh. A pioneer of the expressionist movement, Van Gogh painted his surroundings as he felt them, not saw them. His art always seems to me like a tapestry mixed with a Crayola drawing. It is this combination of the rich and emotive, with the simple and playful that makes Van Gogh’s work so popular. Starry Night is one of the best examples of this. The rolling night sky almost pulsates with movement. The stars and moon shimmer, like rippling reflections in a pool. The fluidity of ‘Starry Night’, what makes it so beautiful, is due to its underlying mathematical structure.

What ‘Starry Night’ is depicting (although this was not a conscious choice by the artist) is turbulent flow; the chaotic movement of water in a dynamical system. It is an incredibly complicated process to model, so much so that mathematicians and scientists today do not have a full solution to the equations. Van Gogh somehow managed to depict turbulent flow in his art.

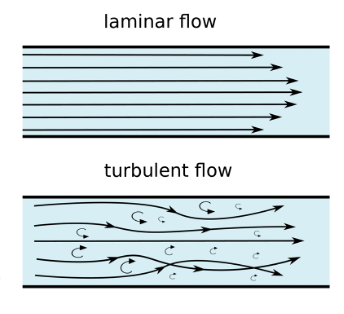
As opposed to laminar flow, where fluids move along nice and neatly in their layers, turbulence occurs when the layers in a moving fluid interact with each other. You can recognise turbulence by looking for eddies (small vortexes). Eddies break off into smaller eddies, transferring kinetic energy into heat, in a process called the energy cascade. Each interaction between layers and particles affects the next, a tiny change in the initial conditions thus being magnified as the fluid continues to move. You may have heard of the butterfly effect – a butterfly flapping its wings in Taiwan can set off a series of events that result in a hurricane in Florida. It is the same principle here. When a small change at the start of something makes a big difference at the end, it becomes extremely difficult to predict the end result; this is called a chaotic system. Chaotic doesn’t mean that it is random, just that there are so many factors or forces going on that we rarely have a full understanding of what is happening.

The problem is we desperately want to know how to predict what is going to happen in a turbulent fluid. Turbulent fluids surround us; water, the atmosphere, even solar flares are determined by it. If we could describe it mathematically we would understand how air moves in our lungs, we could make wind turbines and dams far more efficient (with renewable energy so needed to help with climate change this would not just be lucrative, it could be lifesaving), we could even reverse hurricanes. If a butterfly can start a storm then a perfectly placed butterfly flapping with just the right amount of force at just the right time could also stop it. Many scientists consider turbulent flow the ‘most important unsolved problem in classical physics’ and the problem is one of the seven Millennium Prize problems.

We do know some things about turbulence. Firstly, we can tell when the flow of a fluid will be laminar or turbulent with something called the Reynolds number (Re). The Reynolds number is the dimensionless ratio of inertial forces to viscous forces in a fluid. Inertia describes the tendency of the universe to be lazy, once a thing is doing something it will keep doing that until an extra force is applied and stops it. If water is moving it will keep moving until something else stops it. Viscosity is that stopping thing, it describes the thickness of a liquid and acts much like friction. Turbulent flow occurs when the Reynolds number is high and inertial forces are dominant; laminar flow occurs when the Reynolds number is low, and viscous forces are dominant. When Re < 10³ the flow is laminar, and when Re > 10⁴ it is turbulent. Of course, this does leave a rather large gap where it can go either way.

Turbulent flow is also described by the Navier-Stokes equations. Described only partially though. The equation is a translated version of Newton’s second law F = ma. For the equations to work we first have to assume we are working with incompressible, Newtonian fluids. This means that both density and viscosity are constant.

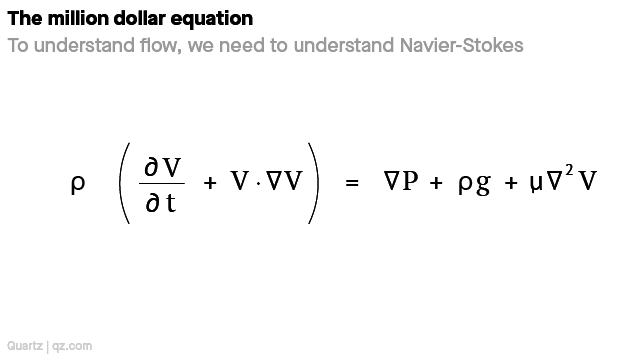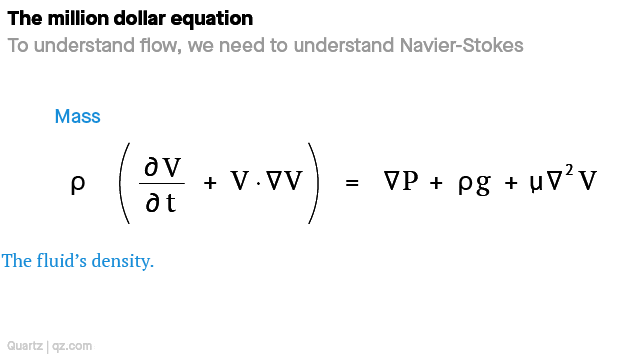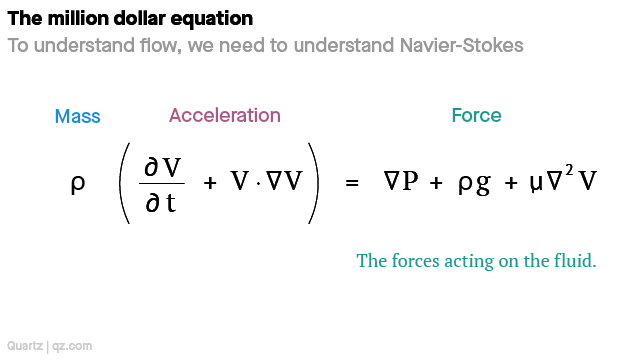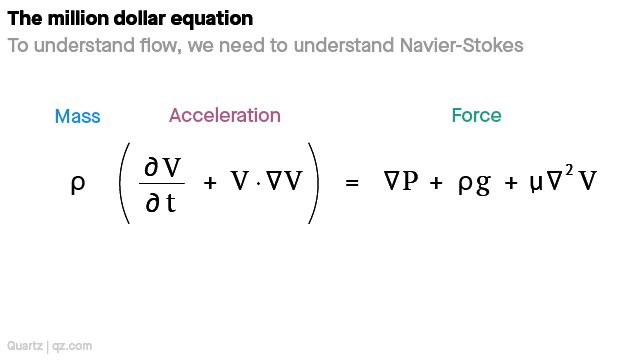
Density (change in velocity over time + speed and direction of the fluid) = change in pressure + external forces (e.g. gravity) + internal forces (e.g. friction)

Mass x (acceleration) = Force

The equation doesn’t describe the lifecycles of individual eddies, but it does give us the overall description of a flow. However, when modelling in 3-D numerical analysis has to be run (computers generating loads of answers for a constant stream of different starting conditions) in order to get an answer, as there are too many undefined variables.

The Millennium prize problem asks to either prove or disprove that:

In three space dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier–Stokes equations.

This is asking, if (when thinking about a 3-D model) we put the equations on a graph, will the graph be globally bound and the gradient be smooth? Put even more simply, will the line have a start and an end, and will it have any breaks or sharp turns?

Looking at the smallest parts of turbulent flow we have the Kolmogorov microscales. These equations tell us what happens in an energy cascade. The equations are universal. They show that how an eddy matures, transforming into smaller eddies and heat, depends solely on the kinematic viscosity (a fluid’s internal resistance to flow under gravitational forces) and the average rate of dissipation of turbulence kinetic energy per unit mass (how fast kinetic energy is spread). The 3 equations show how the energy cascade scales (compares with the start) with length, time, and velocity.

Turbulent flow is evidently extremely complex. Moreover, it is so complicated it is practically pattern less. So, it stands to reason that Van Gogh should not have been able to recreate the phenomena accurately. But while he did not solve the Navier-Stokes equations, he was mathematically near perfect in his application of paint.

How do we know? In 2004, when observing the eddies of a cloud of dust and gas deep in outer space using the Hubble telescope, scientists were reminded of ‘Starry Night’. Jupiter’s red spot set off the same associations. They followed up on this partnership and started to analyse Van Gogh’s work. After digitalising many works they determined that the probability of two pixels a certain distance apart having the same luminosity (this means tone not colour) had Kolmogorov scaling in its probability distribution.

However, this extraordinary relationship is only present in the artist’s periods of psychotic agitation. ‘Self-Portrait with Bandaged Ear and Pipe’ was painted just after ‘Starry Night’, yet the smoke from the pipe in the former is nothing like the rolling night sky so loved in the latter. The difference is that the artist was on medication whilst working on this portrait. As is evident from the bandaged ear, he had recently suffered a severe mental breakdown, and was living in a mental hospital. Describing himself as being in a state of ‘immense calm’ while painting, the pipe’s smoke flows regularly, in a laminar fashion.

It is no coincidence that Van Gogh’s turbulent art mirrored a turbulent mind. Genius has always been linked to madness; the Greek’s term for both was ‘touched by the gods’. We think that Van Gogh had a range of mental dysfunctions and illnesses, which included bipolar disorder and bouts of psychosis. Bipolar disorder reduces brain activity in the lower part of the frontal lobe and increases it in the higher part. This is the same shift that is observed when people have bouts of creativity. Psychosis loosens the mind, allowing contradictory ideas to be held simultaneously, and making people conscious of what would normally be vague, subconscious, links between ideas. Psychosis can thus make people more creative.  It is not an exact match, but it is interesting to note that the other two artists mentioned in this essay likely had some/the same mental dysfunctions. Jackson pollock suffered from alcoholism and bipolar disorder. Hokusai, though undiagnosed for anything, moved 92 times in his life and changed his name over 30 times (indicative of an unstable mind).

Dysfunction of the brain explains why some artists have a ‘feeling’, or intuition, for maths. What it does not explain is why the viewer does too. When comparing work from Van Gogh’s periods of mental agitation to those when he was medicated, the former is simply better. The pieces are more fluid, more emotive, and ultimately more successful.

Whilst maths models the physical world, art visualises our emotive world, and does so by appealing to our sense of beauty. And clearly there is a link between maths and the emotive. Indeed, any artwork broken down is just a mix of mathematical components. Shapes are geometry, composition is symmetry and proportion, and colour theory can be understood as ratios in correspondence with the colour wheel. It must be true then, that beauty, at least in art, is somewhat dependant on an inherent appreciation of mathematics.

Copyrighted images have been used in this essay under Fair Use as:

1. They illustrate an educational article about what the images represents.
2. The images are used as the primary means of visual identification of the article topic.
3. Images are at a low resolution.
4. Their inclusion in the article adds significantly to the article because the print and its historical significance are the object of discussion in the article.
5. They are not replaceable with an un-copyrighted or freely copyrighted image of comparable educational value.