Amelia Tan

A Tangent about Tangents

By: Amelia Tan

1 Introduction

Hello dear reader, thank you for being here! Perhaps by mentioning Pierre de Fermat, René Descartes, and (for lack of better word) a petty mathematical feud, just perhaps you will make the connection with the title and know what I will be writing about. And if so, you can just skip this essay entirely! But perhaps you don’t and you’re up for a little history lesson, and you’ll call me a liar because “this is supposed to be an essay about mathematics”, never fear, there will be plenty of maths in this essay. However, this tangent of an introduction is getting too long. So, let us embark on a journey through time.

Descartes is widely renowned for his pioneering in analytical geometry, which is the ability to represent an algebraic equation onto an x-y plane, also known as the Cartesian plane (Des CARTES, CARTESian, do you see it! ).

Descartes shared his findings with fellow mathematicians , which is how his work circulated into the Fermat’s hands, a French Judge, who solved math puzzles in his leisure time (*gasp, one of the greatest mathematicians in history was in fact not a scholar) [1]. Anyways, Fermat criticised aspects of Descartes work, and Descartes was deeply offended that a maths hobbyist should criticise his work when he was so obviously superior, marking the beginning of a mathematical rivalry!

2 What is a Tangent

Let’s take a detour to define what a tangent or tangent line is (not the function tangent of x, nor to go off on a tangent).

A tangent line, defined by Leibniz, is “a line through a pair of infinitely close points on the curve”. Well, that’s an awfully unhelpful definition, so let’s break it down. Firstly, a curve is a smoothly drawn line or shape, like a parabola or a circle. Next, what does Leibniz mean when he refers to infinitely close points? Really that is just a confusing way to say the tangent line touches the curve at one point but does not intersect it. To visualise this, I’ve inserted the graph of 𝑦 = 𝑥² (red line) , and a straight green line which is tangent to the curve. We say that it is tangent to the curve since it touches 𝑦 = 𝑥² at precisely (1,1) and nowhere else.

Side note : I am realising that Leibniz’s definition may not be the most fitting given he was about 4 years old when Descartes died, but we’re going to ignore that for now.

3 Two Differing Methods

So, how do tangents come into play between Descartes and Fermat? In 1637, Descartes wrote what he considered his greatest findings in his book La Géométrie , where he penned his method to find the tangent to a curve. At the same time, Fermat had also come up with his own method of tangents. Given differential calculus wasn’t invented till around 1665, both their methods are quite clever, though not to spoil the fun, but one was most definitely cleverer than the other. I will outline each method in 3.1 and 3.2.

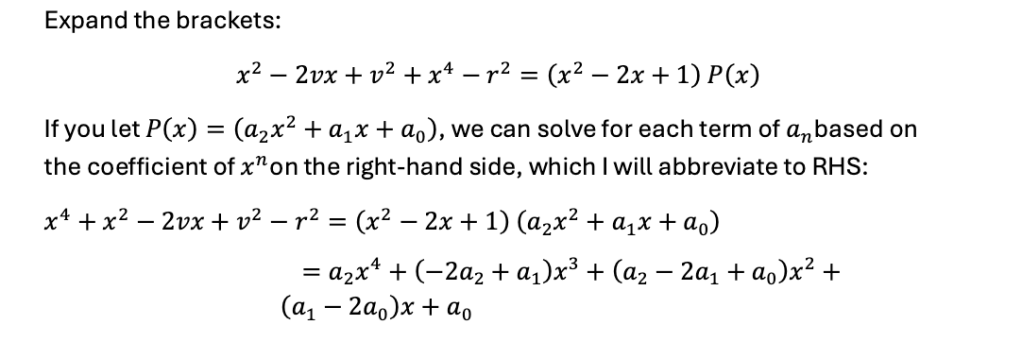
3.2 Fermat’s Method of Tangents

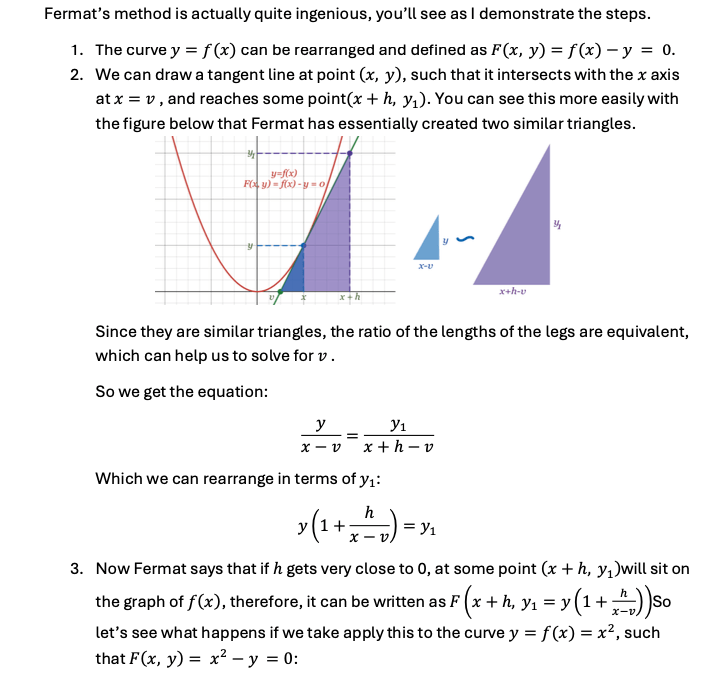
4 Lines of Conflict

When Fermat received Descartes’ method on tangents via Mersenne (another famous mathematician), he criticised Descartes for being overly complex and convoluted , and requested that Mersenne show Descartes his own simpler method.

Descartes was particularly known for being a confident mathematician, if not a bit self – important. He abhorred the idea of Fermat attacking his work when he was m ore established in the field than Fermat.

Particularly, in some correspondence with Mersenne, Descartes called Fermat’s method “nothing more than a false position , founded on a means of demonstration that reduces to the impossible, and that is the least valued and the least clever of all of that are used in mathematics . Whereas mine is drawn from a familiarity with the nature of equations that were never explained …” [2]

Mersenne relayed this to Fermat, who defended himself saying his method was “just as certain as the construction of the first proposition of the Elements . Perhaps having them put forward naked and without demonstration, they were not understood, or they appeared too simple to M. Descartes, who has made so much headway and has taken such a d ifficult path for these tangents in his Geometry.” [2]

In light of such conflict, Descartes wished to disprove Fermat’s method by proposing the curve, now known as the Folium of Descartes , and challenging him to find the tangent line on any given point as Descartes had failed to do so with his own method.

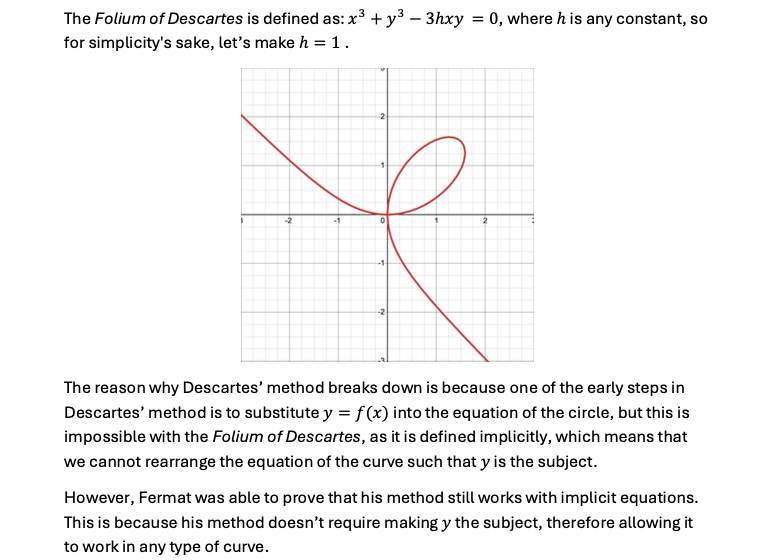
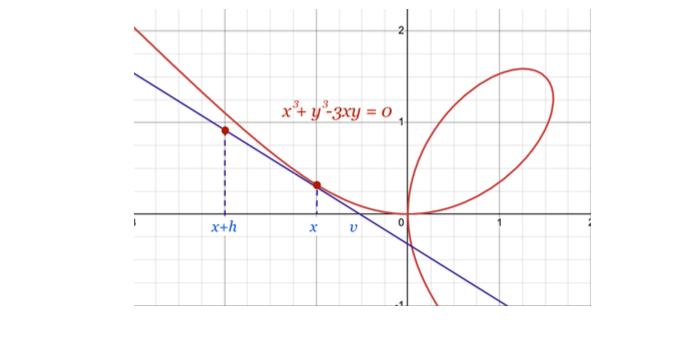
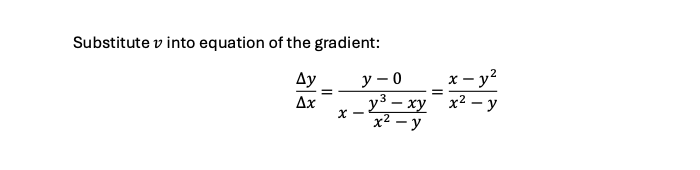
5 Conclusion

I hope you enjoyed this ride through mathematical history. Perhaps I strayed a bit away from tangent lines, but that’s why this essay is called a tangent in the first place (sorry this joke is getting old)!

Maybe all the math we did today is completely useless , but it is fascinating to see the first inklings of differential calculus in Fermat’s work and see the absolute genius of his method. It is so rare that we get to deep dive into the beginnings of mathematical ideas (outside of perhaps how we used to approximate pi) and as a lover of analytical geometry and calculus, this was very fun to research! I find it fitting that I should write an essay about tangents, as my math teacher has made plenty of puns with my last name ‘tan’ and tangent lines or the tangent function . Anyway, t hank you for directing your eyes normal to your computer screen to read what was on it, when we intersect (meet) again! I hope that your tangent is at the point of inflection, so we are sure to cross paths …

References

[1] Kumar, S. (2021, May 17). Fermat, Descartes, and The Dawn of Differential Calculus. Cantor’s Paradise. Retrieved April 4, 2025, from https://www.cantorsparadise.com/ fermat -descartes -and -the-dawn -of-differential -calculus -80472d35c0c1

[2] Skinner, L. (2015). The World Before Calculus: Historical Approaches to the Tangent The World Before Calculus: Historical Approaches to the Tangent Line Problem. WWU Honors Program Senior Projects. https://cedar.wwu.edu/cgi/ viewcontent.cgi?article=1012&context=wwu_honors

[3] Descartes, R. (2013). Selected Correspondence of Descartes (J. Bennett, Trans.). Early Modern Texts. Retrieved April 4, 2025, from https://www.earlymoderntexts.com/assets/pdfs/descartes1619.pdf