This is one of my favourite Maths questions. I encountered it among a list of past interview questions for Oxbridge admissions: how can we get from point A to point B using the edges of the cube, without going over the same edge twice?

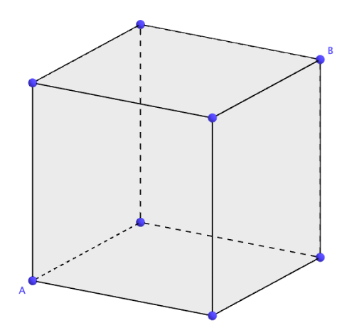
I encourage you to try it yourself first, as getting to the solution gave me another glimpse at the beauty of Maths problem solving. And who knows? Maybe you’ll get to a different solution than the one below…

Now, let’s take a look at my process for coming to a solution. I often look at beautiful solutions and think to myself ‘how on Earth did they come up with that?’ So, I’ll show you my exact steps.

First, we need a way of representing the road we take from A to B. Since we can represent an edge by stating its two endpoints, let’s try to label all the vertices of the cube. The natural way to do that is with the standard 3D Cartesian coordinates.

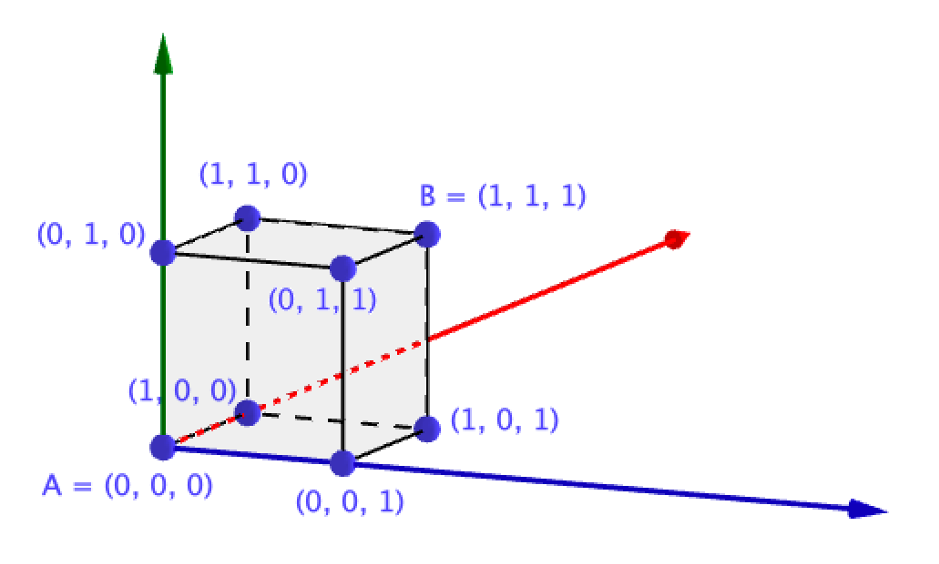
As you can see, A is chosen to be the origin of the coordinate system. Also, for ease of notation B was chosen to be the point (1, 1, 1), which can be done without changing the problem (all we are doing is re-scaling the cube to have side length 1 which doesn’t affect the number of paths).

It was at this point my friend remarked that the cube was too hard to visualise on paper, which made me realise that we don’t actually have to visualise it in 3D. The only information we need is how the points are connected together – ie. where we can move to from a given point.

So, picking a random point say (1, 0, 1), where can we move? Looking at the diagram you can see that there are three points connected to this point: (1, 1, 1), (1, 0, 0) and (0, 0, 1). From here it is not too hard to deduce that any two points are connected by an edge if their coordinates are different in exactly one place (only in x, y or z from (x, y, z)). And we can use this to show the lines in a 2D way as follows:

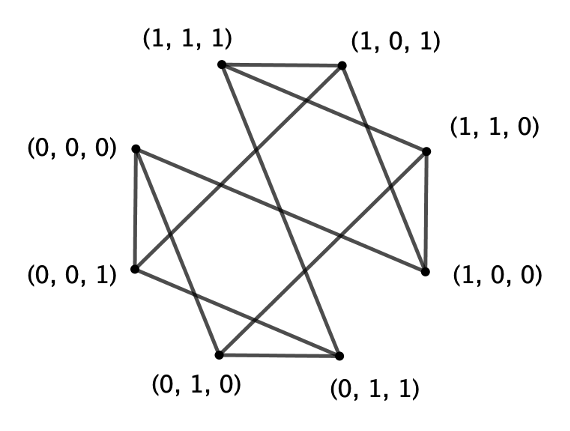
Next, we need some logic for the way we arrange these points in a diagram. In other words, we need more symmetry in the picture. A cube is very symmetric (48 symmetries in total – can you work them all out?) and so our 2D representation should ideally be more symmetric. This was my second attempt:

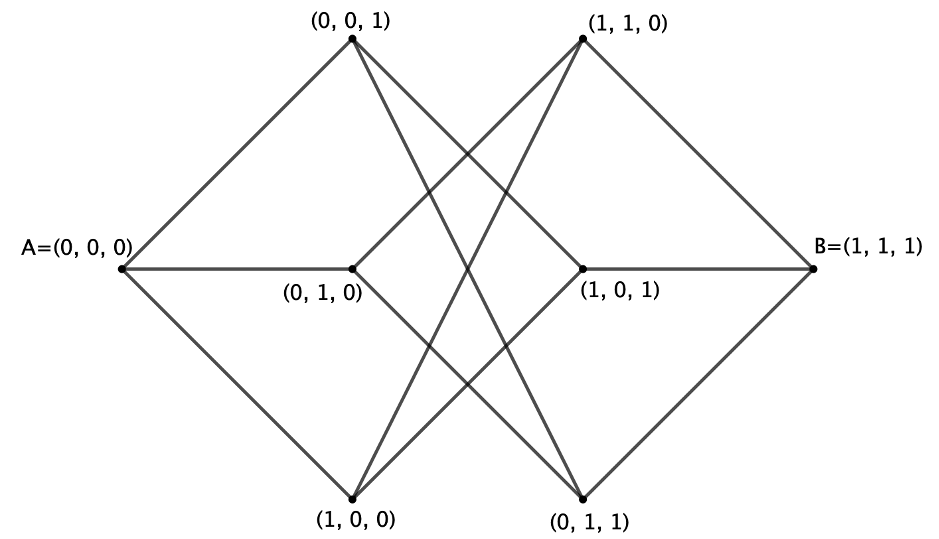
…we can do better than that. The central part in the next one is less jumbled.

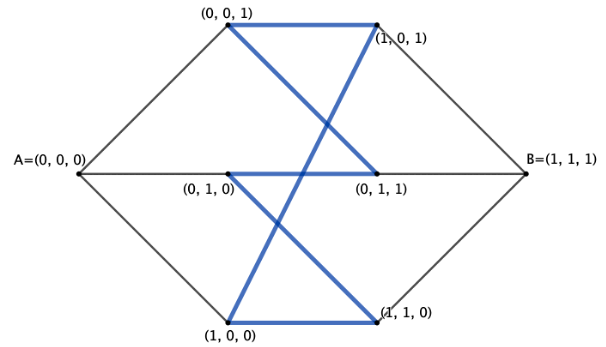
Now we’re getting somewhere. Do you notice something in the middle? The path in blue looks like a crumpled hexagon – what would happen if we unravelled it?

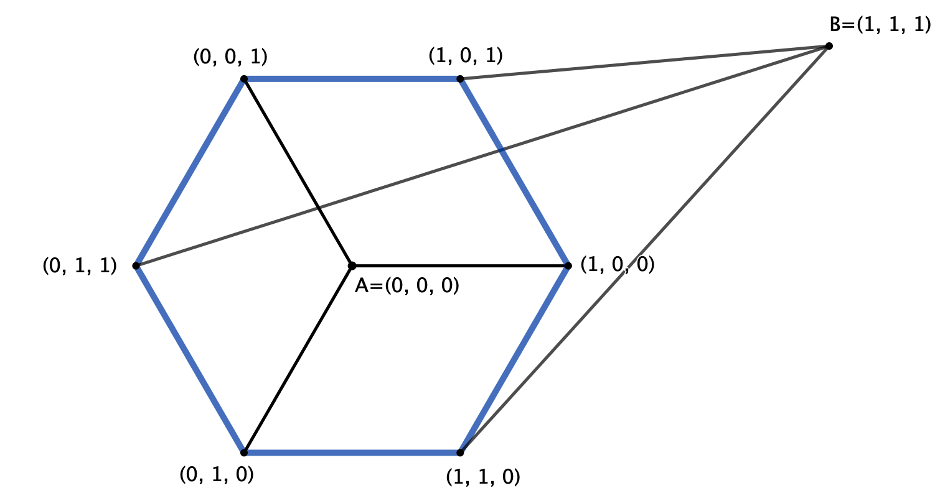
Much better. I’d say we’re almost at the point where we can start counting the ways to get from A to B, we just have a couple of little problems to iron out…

First, B is not symmetrical in the picture. Sure, you could say this is only an aesthetic thing, but symmetry in Maths often helps us to solve things more easily so let’s try to fix it. One idea would be to add 3 ‘B’s into the picture – one for each of the nodes connected to it. But, thinking about this a little deeper, we see that because the path has to end at B – and once we are there we cannot go back – then in fact B does not need to be connected to the rest of the picture. Instead, we can just draw some EXIT signs at the nodes connected to B. Once you reach one of these points, you have two choices: either “exit” the picture through a B (only one way to do that: move to B from that point), or continue along the hexagon. This observation will be very helpful when it comes to counting paths.

Second, we are not quite sure where to go from A. There is no obvious choice for a starting move. From A to… which of the three? Thankfully, due to the symmetry of the picture (and of the problem, of course), we can simply count the ways to get from A to B with the first move being ‘A to (0, 0, 1)’ and then multiply by 3 to get the result. So, let’s do exactly that!

Given our new-found knowledge, we can make very useful simplifications to the picture. Firstly, the line from A to (0, 0, 1) can be replaced simply by an ENTRY sign at (0, 0, 1), since that is our starting move (which we do in exactly one way). Secondly, since we cannot use that first line anymore, we can simply remove it.

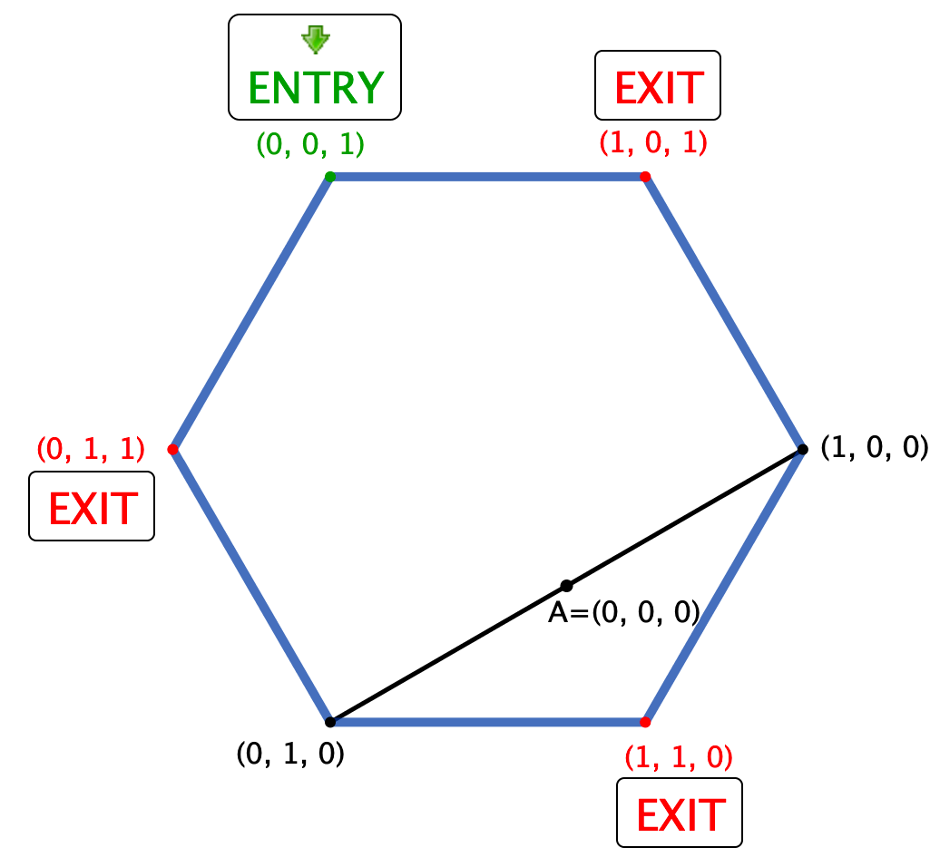
Now things are really starting to take shape. In this form we see that the line through the point A is equivalent to just going from (1, 0, 0) to (0, 1, 0) or the reverse (once we are in A, we cannot go back to where we came from), and so we can simply delete the point A. Also, for neatness, let’s rotate the whole diagram 60 degrees clockwise.

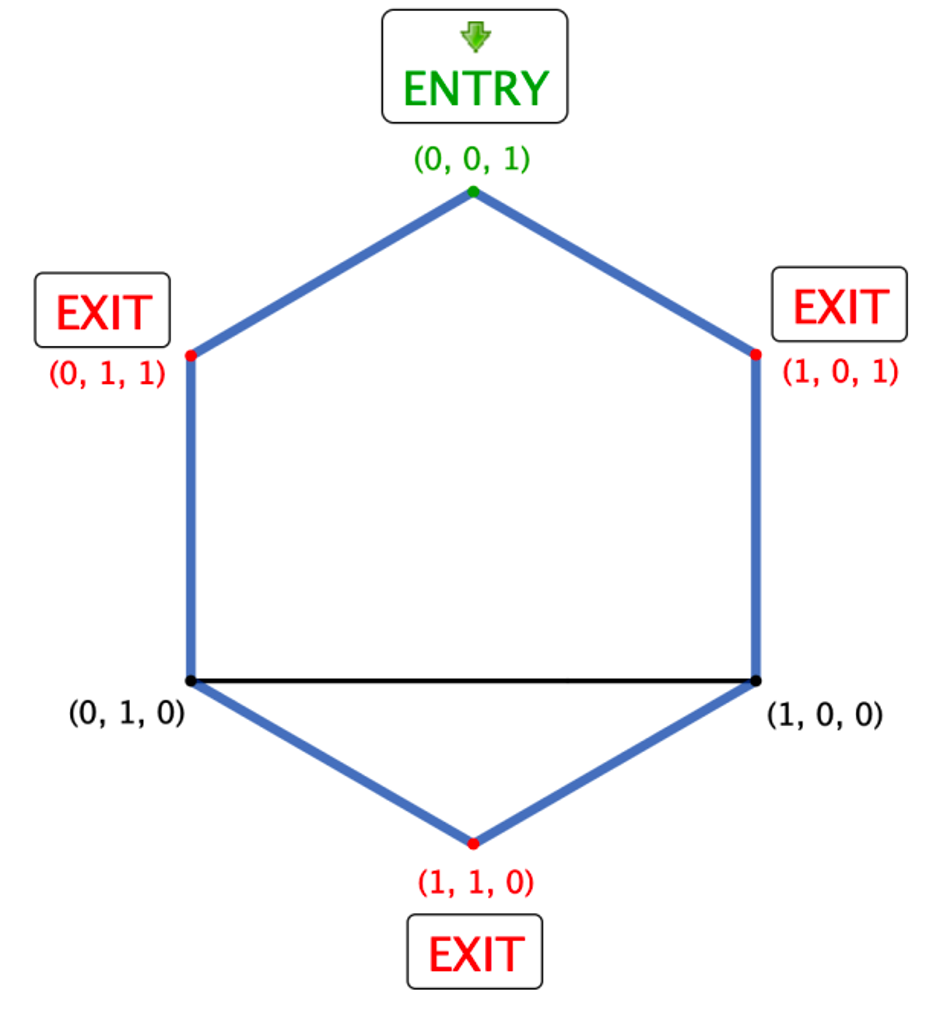
Perfect! I’d say we are now in a position to start counting paths – remembering that we have to multiply by 3 at the end because of the symmetry of the first move. In fact, looking at our much simplified – and very symmetric – diagram, it becomes apparent that we can also count all of the paths that start by going from the ENTRY POINT to (1, 0, 1) and then multiply by 2 at the end. I told you symmetry was going to be helpful!

The following picture should help with the counting:

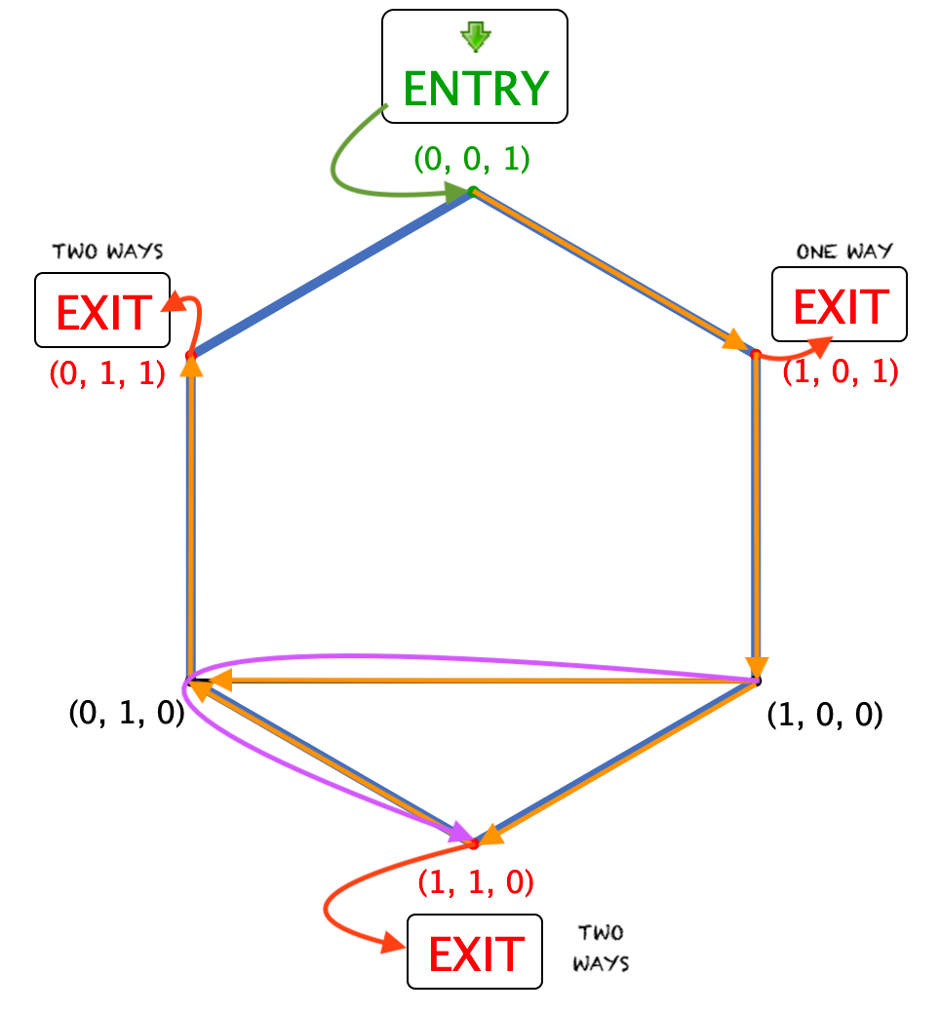
It perhaps looks a little complicated so let’s break it down. Following all the arrows, or doing it on your own, you can hopefully see that by going through an edge once and starting as decided above (ENTRY to (1,0,1)), we have the following:

• one way to get to the (1, 0, 1) EXIT
• two ways to get to the (1, 1, 0) EXIT (ah, that pesky purple arrow!)
• two ways to get to the (0, 1, 1) EXIT (either only on the hexagon, or using the shortcut).

In total, with the chosen start, we have 5 ways to get from A to B. But, don’t forget we need to multiply due to the symmetries that we’ve used to simplify the problem. First, multiply by 2 (we can go to (0, 1, 1) instead of (1, 0, 1) starting from (0, 0, 1)) and get 10 ways. And then multiply by 3, the number of ways to choose an ENTRY point. Thus, the actual total is 30.

ANSWER: 30 Ways to get from A to B!

Whilst we take a well-deserved moment to pat ourselves on the back for getting the right answer, let’s look at some things to take away from this problem.

1. Even if you are asked about a cube in a problem, you mustn’t get stuck on the idea of a cube. Maths is flexible that way. You can model your cube into any other structure that keeps the important elements in place. In our case, only the ways in which the vertices were connected mattered, not the angles between the lines or anything. Thus, a graph was a fairly good choice.
2. You can sometimes make use of the symmetry of a problem to make your life easier, as we did with the way we counted the total number of paths. Symmetry plays a very important role in Mathematics, so keep an eye out for it.

I hope you enjoyed my solution and best of luck with your own Maths problems! If you want to discuss something, leave a comment below – this place is always open to interesting solutions or remarks.

The original version of this article can be found here.

Vlad Tuchilus