Nanfan Yi

We have seen that infinity/the infinite can be used to answer the “how large” and “how many” questions in the last article starting only from dots and lines. Here, we start at the exact same point (pun intended). In the first article we concluded that there are infinitely many points on a line. Now we may define a number line by identifying each point on the line as a number:

Does this mean we have infinitely many numbers? Perhaps you have started thinking about it before when counting 0, 1, 2, 3, 4, 5, …, 100,…, 100000… We could identify more points by going further to the right. These numbers are what we call “natural numbers”, where “natural” comes from the sense that we count quantities using them. There are infinitely many natural numbers, but they are not the only “residents” on the numberline.

All the numbers with corresponding points on the entire numberline are called the real numbers. The real numbers include irrational numbers (cannot be put into a fraction and have infinitely many digits after the decimal point) and rational numbers. Rational numbers (can always be put into a fraction) also include the integers, and the integers include the natural numbers.  

Now you can hopefully see that each collection of numbers (we call them sets) has infinitely many numbers, as they all include the set of the natural numbers and more besides. John Green claims that some infinities are bigger than the others in The Fault in Our Stars. Mathematically speaking, this is an issue of “countability” – whether or not a set of numbers can be counted in the same way as we count the natural numbers. If yes, then this set is countable; if no, then it is uncountable.

It is straightforward to see how the set of non-negative even integers is countable: imagine I count 0, 1, 2, 3, … and you count my numbers doubled 0, 2, 4, 6, … at the same time:

0 →  0

1→ 2

2 → 4

3 → 6

…

n → 2n

…

From this, we see the set of non-negative even integers is countable. Neither of us is going to run out of numbers as we both have infinitely many of them and hence by doubling you will count as many non-negative even integers as I count the natural numbers.   

Now if you count the number by doubling mine and adding 1, then we could “count” the non-negative odd integers as well:

0 → 2*0+1 = 1

1 → 2*1+1 = 3

2 → 2*2+1 = 5

3 → 2*3+1 = 7

…

n → 2n+1

…

It does take a little more more effort to see how the set of integers is also countable. The numbers I count are in orange, and those you do are in black. 

For 0, we both count 0. For every odd natural number “x” I count, you count the corresponding number by doubling then minus 1: 2x-1. For every even natural number “y” I count, you count the corresponding number by multiplying by -1/2: -1/2y. We then construct the following zigzag:

As the zigzag continues, my counting would include all the natural numbers, whereas yours would include all the integers! In addition, I circled the orange numbers on purpose. We could view the integers in an infinite list indexed by the natural numbers, or as the 1st, 2nd, 3rd, 4th,…, nth,… stop of the zigzagging journey. 

More surprisingly (for me at least) the set of rational numbers is also countable. An elegant proof can be found again using the zigzag approach. If you have a piece of paper, and a pencil/pen, you can do it as well (and I strongly encourage you do!). Let’s prove the countability of the positive rational numbers:

1. Construct a table with infinite dimensions like this:

2. Go zigzagging! Remember to skip those which have the same irreducible fraction as those already counted (for example, 2/1 and 4/2 are both equal to 2 and so we skip 4/2):

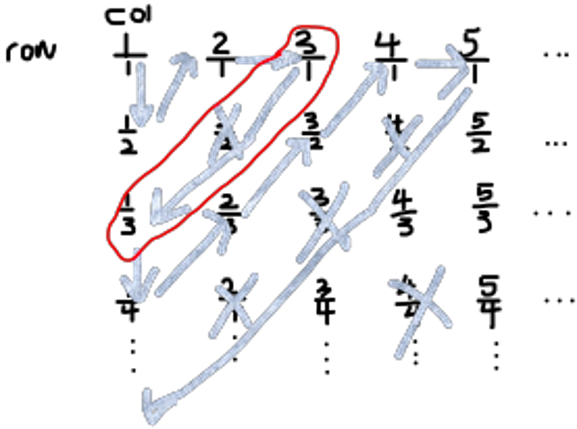
3. Assign each “stop” of the zigzag line with a natural number. Can you see how this completes the proof? Let’s count them together…

The trick is to not go along the horizontal/vertical direction but rather a “diagonal” one. This is because by going horizontally or vertically our zig-zag line may never come back to “pass through” the other rational numbers, it will just continue forever to infinity! Whereas, for each of the “diagonals” (example in the red circle), they have ending entries (i.e. 3/1 & 1/3), and so we know the zigzag is jumping to the next diagonal at one of the ends (above). Eventually, the zigzag will “pass through” every positive rational number, meaning we can index them by the natural numbers (countable!).

We can also do the same zigzag on the negative rational numbers by adding a “-“ sign in front of every number in the table below…

Now, if we start with 0 (0th stop), index the positive rational numbers with odd natural numbers (1st, 3rd, 5th,…stops), and the negative rational numbers with even natural numbers (2nd, 4th, 6th,… stops) we have a valid solution – the rational numbers are countable!

So far we’ve shown the integers are countable, and the rationals are countable, which just leaves the reals. Can we write the real numbers down like we did above and count in the same way we do with the natural numbers? Well, suppose we write down such an infinite list which includes all the real numbers that are indexed by the natural numbers:

Look at the diagonal entries: if we replace them by adding 1 to the current entry (i.e. 0 → 1, 1 → 2, …, 9 → 0):

…we’ve created a number that is real BUT not on the list (because it always differs in at least one entry)! Which means that our assumption that we can number the list of real numbers with the natural numbers must have been wrong. Therefore, this set is uncountable! And this infinity is “larger”!

We’ve now seen how despite all having infinitely many terms, we could count the integers and rational numbers the same way we count the natural numbers, but we cannot do the same thing to the real numbers because there are will always be even more real numbers floating out there!

 

You can read the next article in the series on infinite series here.

 

*********Sidebar Talking**********

The last proof was a genius idea from Georg Cantor, and we call it a “diagonal argument”. You can read more about it here.

Georg Cantor was a German mathematician who created a branch of mathematics called set theory. In this article we’ve touched on how a “set” is a collection of stuff, i.e. the set of natural numbers is the collection of 0, 1, 2, 3, … He also decided to call the size of a set the “cardinality”. Rigorously speaking, saying that a set is countable means the cardinality of this set is equal to the cardinality of the set of natural numbers. Thinking about it naively, the sets of natural numbers, integers, rational numbers, and real numbers all have infinite cardinalities. Still, the cardinality of the real numbers is the largest among all. That is why we say “some infinities are bigger”.

Georg Cantor defined the cardinality of the set of natural numbers to be aleph-null and the Continuum Hypothesis states that the cardinality of the set of real numbers is aleph-one. However, aleph-one is not the “largest infinity” in set theory. Confused? Read more here and I guarantee it will be more confusing but slightly interesting, only slightly 🙂