Harriet Wood – student winner of the 2020 Teddy Rocks Maths Essay Competition
Notes on honeycomb and M.C. Escher
“Triangles are my favourite shape, three points where two lines meet … let’s tessellate”
– Alt-J
Have you ever noticed patterns in the brickwork of the pavement as you’re walking into town? Or in the wallpaper at your grandparents’ house? Or in the quilt on your bed? Most people have at some point in their lives noticed the beauty of the patterns in the world around them. However, many don’t realise that this beauty is in fact mathematics.
You will often hear mathematicians say that maths is beautiful. At first, it can just seem like they’re referring to the perfection of a nice proof when it comes to its conclusion. But it is much more than this – ask a mathematician which part of maths they find the most intrinsically beautiful and you’ll receive a wide variety of answers, each very individual to the person. For me, this beauty is found in tessellation. From my favourite book as a child Penrose the Mathematical Cat to the video series Doodling in Math Class by Vihart in teenage years, the beauty in this form of mathematics has always fascinated me.
Tessellations can be found everywhere: in the periodic arrangement of hexagons in honeycomb, stained-glass windows and mosaic tilings, and the striking artwork of M.C. Escher. They have even made their name in popular culture, from tiling puzzles and the tangram to the video game Tetris, where the aim is to create tessellations as best you can from a set of falling tetrominoes.
A tessellation is defined a repeating pattern made of one or more shapes, without the formation of gaps or overlaps. As an art form, tessellation is particularly rich in mathematics, with ties to geometry, topology and group theory.

The simplest types of tessellation are referred to as regular tessellations. These are monohedral tilings (where every single tile is congruent) of regular polygons (all having equal sides and angles). From the fact that angles around a point must sum to 360 degrees, it is easy to infer mathematically that there are only three types of regular polygons which can make up these tessellations – equilateral triangles, squares, and regular hexagons. This is because these are the only regular polygons with internal angles that are a factor of 360 degrees.
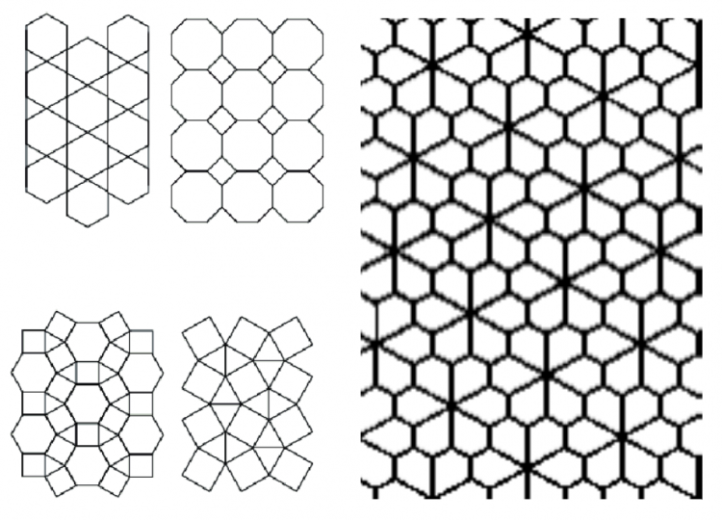
Other common types of pattern are semi-regular tessellations, which allow more than one type of regular polygon as tiles, or monohedral tessellations, which only use congruent tiles. Within nature, tessellations tend to be regular or semi-regular.
Honeycomb has such a regular tessellation to allow for the most efficient construction, allowing multiple bees to build different cells at one time. This is because each cell is exactly the same. However, this still leaves the three options for the shape – a square, triangle, or hexagonal cell. In 1999, the mathematician Thomas Hales proved the ‘honeycomb conjecture’, which demonstrated that the hexagon provided the least total perimeter out of these three options. This can be easily demonstrated for hexagons and triangles. Take the side length of each small triangle above to be one unit. The perimeter of both of the shapes is exactly the same – each is made up of six edges of the small triangles and is therefore six units in length. However, you can clearly see that the hexagonal shape provides a larger area, fitting six triangles as opposed to four. It’s more difficult to see this with squares in comparison to hexagons, however again if you construct a square with the same perimeter, the hexagon again has a greater total area as it is rounder in shape. Evolutionarily, this provides an advantage to the bees as less beeswax is needed overall for the same area of construction.
Take the side length of each small triangle above to be one unit. The perimeter of both of the shapes is exactly the same – each is made up of six edges of the small triangles and is therefore six units in length. However, you can clearly see that the hexagonal shape provides a larger area, fitting six triangles as opposed to four. It’s more difficult to see this with squares in comparison to hexagons, however again if you construct a square with the same perimeter, the hexagon again has a greater total area as it is rounder in shape. Evolutionarily, this provides an advantage to the bees as less beeswax is needed overall for the same area of construction.
At a molecular level, tessellation can also be found, especially within crystal structures. Single molecular units can act as tiles and combine to build complex three-dimensional molecular tessellations; properties of these tessellations such as their geometric symmetry can help scientists understand self-organised systems in biology and nanotechnology – especially as more and more complex tessellations are found.
As of yet, all the tessellations we have looked at have been periodic; that is, a tiling that has a repeating pattern within itself. If you walked along a surface with this kind of tiling, you would be able to easily predict what comes next.
However, there is such a thing as an aperiodic tiling – one which uses a small set of tile shapes that cannot form a repeating pattern, no matter how large the area. If you walked along an infinite surface with this kind of tiling, no matter how long you walked for, you would never be able to predict what comes next.

In 1967, the British mathematician Roger Penrose was interested in crafting this infinite variation. In order to achieve this, he couldn’t use any tiles with two, three, four, or six axes of symmetry; on an infinite plane this symmetry would ultimately result in periodic patterns. So, Penrose used five-axis symmetry, or the pentagon – a shape which was believed to always leave gaps in the tiling of a plane.
Penrose made several versions of these aperiodic tile sets, the first of which uses pentagons and three other shapes (a “star”, “diamond” and “boat”) and a set of rules to ensure that all tilings are non-periodic. The second involves just two shapes – the ‘dart’ and the ‘kite’, with the matching rule that the placement of the two symmetrical arcs on their surfaces has to line up, creating continuous curves. These Penrose tilings, despite never having translational symmetry (repeated sections), may have both reflectional symmetry and fivefold rotational symmetry. This is known as so-called “forbidden symmetry”, because it goes against the unconscious association humans have between repetition and symmetry.

In the second type of Penrose tiling, the ratio of the area of the kite to that of the dart is the golden ratio. The ratio of the longer side of the kite to its shorter side is also the golden ratio. And, finally, in an infinite plane, the ratio of the number of darts to kites is also the golden ratio. This ratio is unavoidable and is one of the mathematical phenomena that emerges everywhere – even where you would least expect it.
Penrose could not have known when he was formulating these tilings that his discovery would have massive significance in materials science. In 1982, Shechtman discovered an alloy with a crystalline structure which didn’t seem to reflect the standard crystallographic symmetries. It was aperiodic – in fact the atoms seemed to be arranged in the same pentagons, kites and darts which Penrose had used in his tilings. For 80 years, the definition of a crystal had been “ordered and periodic”, but this discovery led to the redefinition of the word entirely.
The unpredictable nature of a Penrose floor makes it appealing for architectural use– for example, in paving the entrance to the Andrew Wiles Building at the University of Oxford. I was fortunate enough to visit this myself recently and I would definitely recommend it.

Mathematicians and non-mathematicians alike have acknowledged the beauty of tessellations and tilings with an almost (and in some cases literal) religious fascination. In 1619, Johannes Kepler wrote Harmonices Mundi, which discussed harmony and congruence in physical phenomena; within the book was an early documented study of tessellation. Kepler reasoned that the relationships he had found gave evidence for God’s design in the world.
He was not the first to make a connection between the ‘harmony’ of geometrical forms and religion – Islamic art had been characterised by its extensive use of geometric and abstract floral patterns for years, especially in religious art forms. In some interpretations of Islam, there is a ban on depiction of animate beings due to the prohibition of idolatry, which led to the focus on expressing the beauty and awe Muslims found in Allah in other ways. In turn, this contributed to the flourishing of mathematical and geometrical tiling within Islamic art.
Mathematics and tessellations have also emerged in Western art forms, most notably in the artwork of M.C. Escher. He was heavily influenced by the tessellations present in Islamic tilings, most notably via his visit to the Alhambra in 1922, where the intricate mosaics triggered his interest in the mathematics of tessellation. What is especially remarkable about the Alhambra tiles is that they contain nearly all, if not all, of the seventeen different possible plane symmetry groups.

He called his works on tessellation Regular Divisions of the Plane, which featured tessellations of reptiles, birds, fish, and other figures in complex interlocking designs. He also combined tessellation with two- and three-dimensional images, such as in the famous print Reptiles.
“The flat shape irritates me—I feel like telling my objects, you are too fictitious, lying there next to each other static and frozen: do something, come off the paper and show me what you are capable of!”
– M.C. Escher

Although Escher didn’t have mathematical training – his understanding of maths was mostly intuitive – he carefully studied the seventeen plane symmetry groups, and then developed a mathematical notation for the symmetry expressed in his own artwork. Later on in life, Escher also became interested by other mathematical concepts – such as infinity, non-Euclidean geometry and impossible objects. For example, inspired by H.S.M. Coxeter, he based his engravings Circle Limit I-IV on the tessellation of a hyperbolic plane. The infinitely regular repetitions of this tessellation, growing rapidly smaller and smaller, allowed him to represent the concept of infinity on a two-dimensional plane.



Escher also used other mathematical concepts to illustrate the idea of infinity in his art – such as the striking Möbius strip with ants walking around and around in perpetual motion. At first the ants always appear to be on opposite ‘sides’ of the strip – but the strip only has one surface; they crawl after each other and travel on both so-called ‘sides’ without crossing the edge of the surface. Therefore, it must be a one-sided shape! The ants could march on forever into infinity. I would definitely recommend Vihart’s videos on the Möbius strip if you want to find out more.
In early 1960, another representation of infinity emerges in Escher’s art: perpetual motion. Along with impossible objects, the images of Waterfall and Ascending and Descending illustrate a fascination with visual paradox and the concept of infinity – both the water and the monks will continue indefinitely in an impossible loop constructed by his imagination.
Interestingly, Roger Penrose (of the Penrose tiling) took a great deal of inspiration from Escher’s Relativity and its impossible perspectives, which led to the formulation of the Penrose triangle and of the Penrose stairs, with help from his father. In turn, Escher was influenced by Penrose’s impossible objects which he incorporated into Waterfall and Ascending and Descending.

Unfortunately, Escher never got a chance to demonstrate his artistic take on the extraordinary tessellation of Penrose tilings – he passed away before their invention. Nonetheless, there is beauty in how their work sits side by side, bringing to mind the very tessellations that Escher and Penrose themselves explored.
Sources
Penrose the Mathematical Cat
Gödel, Escher, Bach
Symmetry, Chemistry, and Escher’s Tiles by Bruce D. Martin and Reza Sarhangi
5 and Penrose Tiling – Numberphile
Why do Bees build Hexagons? Honeycomb Conjecture explained by Thomas Hales – Tom Rocks Maths
Impossible Cookware and Other Triumphs of the Penrose Tile by Patchen Barss
The Official Website of M.C. Escher
Tessellation from Wolfram MathWorld
Tessellation in puzzles and recreational mathematics – Wikipedia
Alhambra in mathematics – Wikipedia
M.C. Escher’s Legacy: A Centennial Celebration
Copyrighted images have been used in this essay under Fair Use as:
- They illustrate an educational article about what the images represents.
- The images are used as the primary means of visual identification of the article topic.
- Images are at a low resolution.
- Their inclusion in the article adds significantly to the article because the print and its historical significance are the object of discussion in the article.
- They are not replaceable with an un-copyrighted or freely copyrighted image of comparable educational value.
You can find more entries from the Teddy Rocks Maths Competition here.
[…] Tessellation, Penrose Tilings and Infinity – TOM ROCKS MATHS […]
LikeLike
[…] Harriet Wood: Tessellation, Penrose Tilings and Infinity […]
LikeLike
[…] 2020 Overall Winner: Richard Zhang2020 Student Winner: Harriet Wood […]
LikeLike