Articles written by interns working with Tom at Tom Rocks Maths HQ in Oxford.

Joe Leach – Abstraction and Graph Theory with Euler

Joe Leach – The path towards higher mathematics is guided by abstraction

Clare Teng – The Legend of AlphaGo Part III: Epic Battles and the Future of AI

Clare Teng – The Legend of AlphaGo Part II: How does it work?
Clare Teng – The Legend of AlphaGo Part I: The Rules of the Game
Iain Duncan – Games of Chance & Game Theory

Iain Duncan – Solvable Games: Theory and Practicality
James Somper – How Chaos Complicates the Solar System

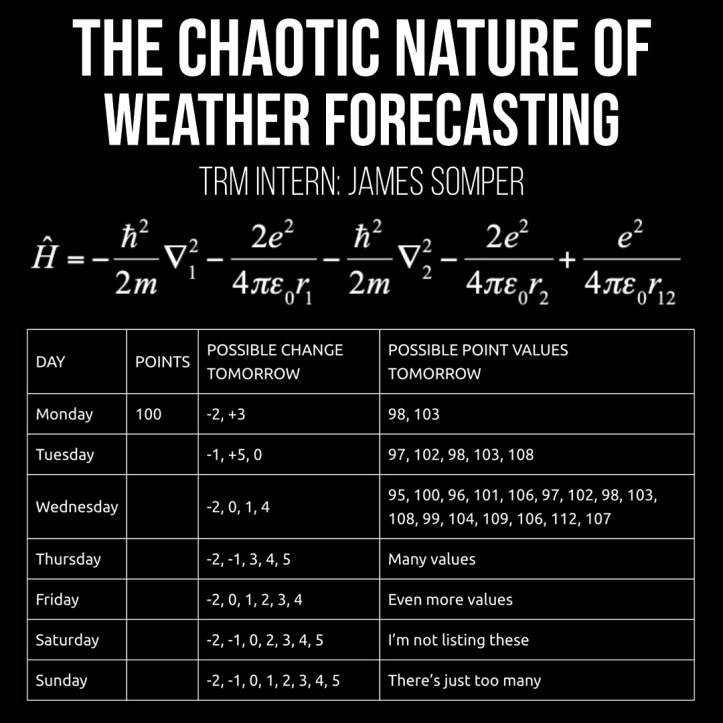
James Somper – The Chaotic Nature of Weather Forecasts
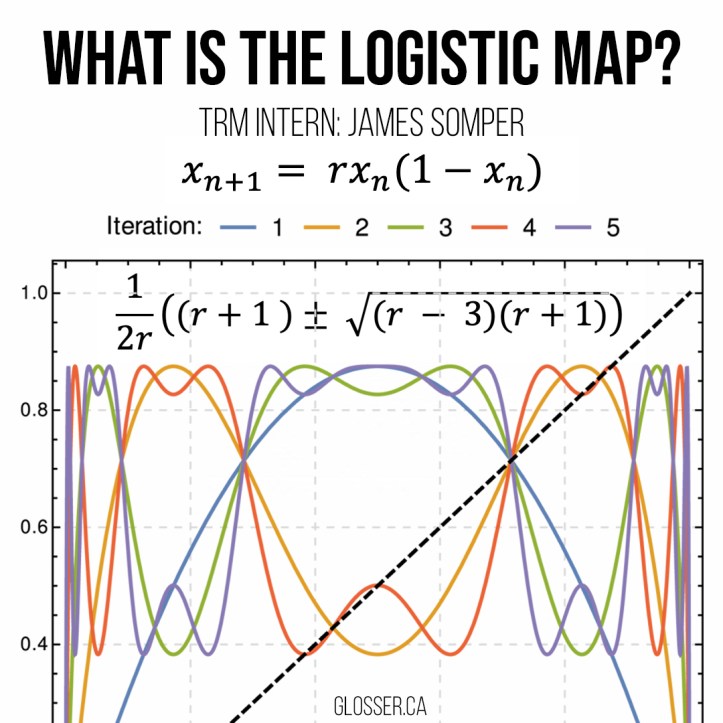
James Somper – The Definition and Properties of Chaos via the Logistic Map
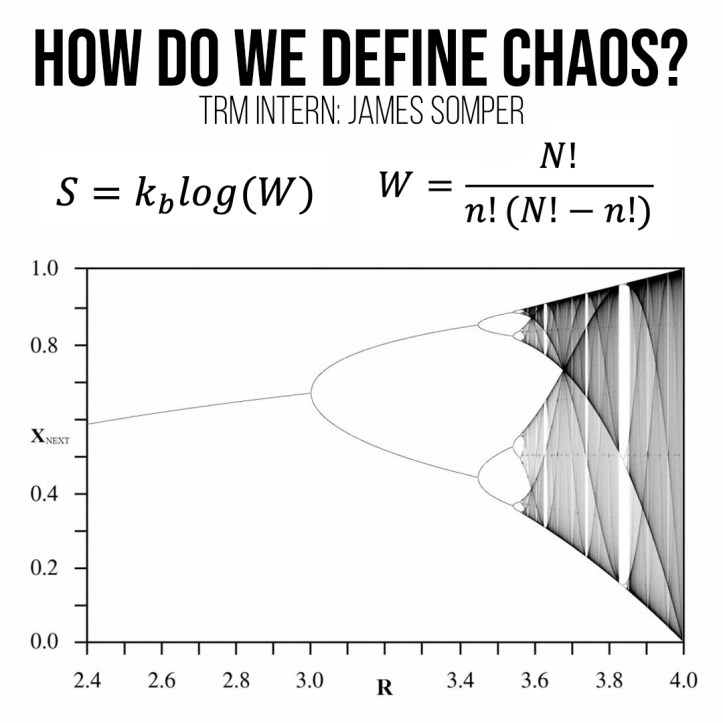
James Somper – A Commencement into Chaos
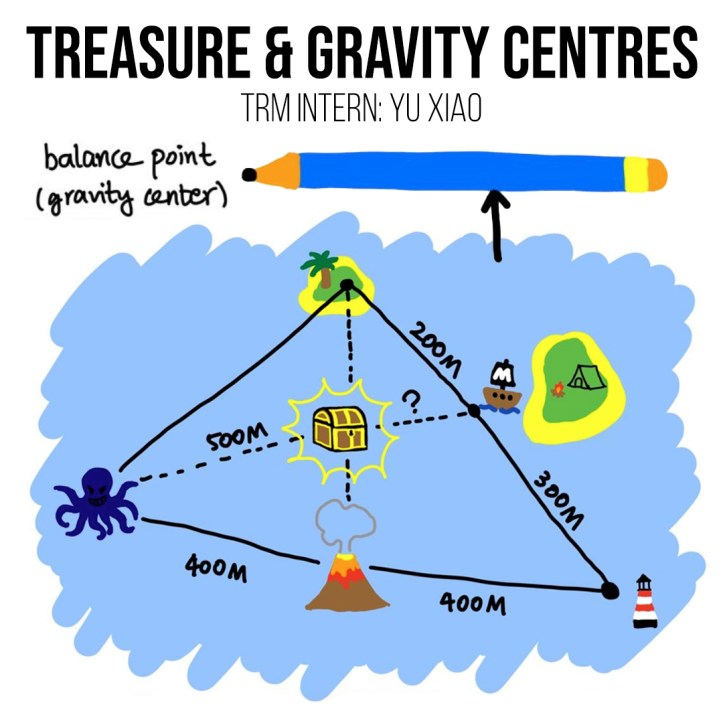
Yu Xiao – Finding Treasure with Gravity Centres
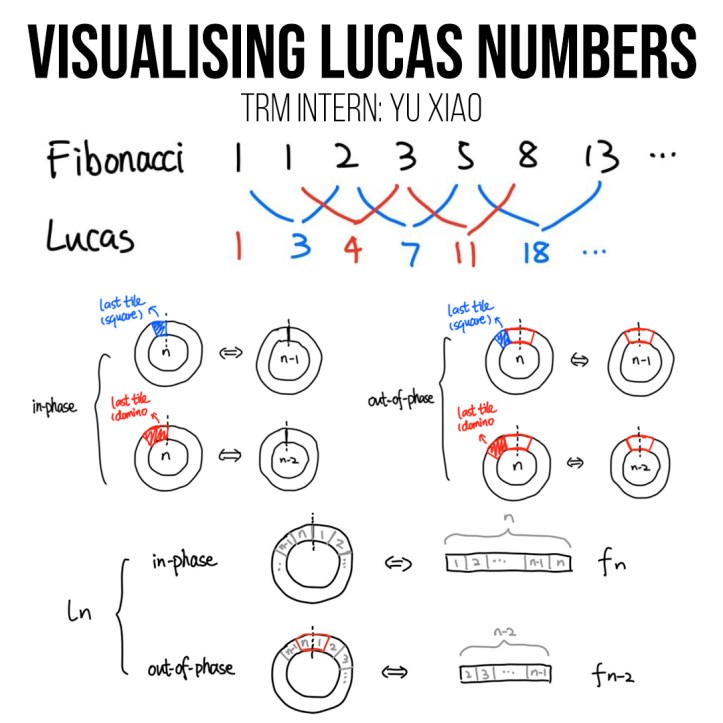
Yu Xiao – Visual Proofs and the Lucas Numbers
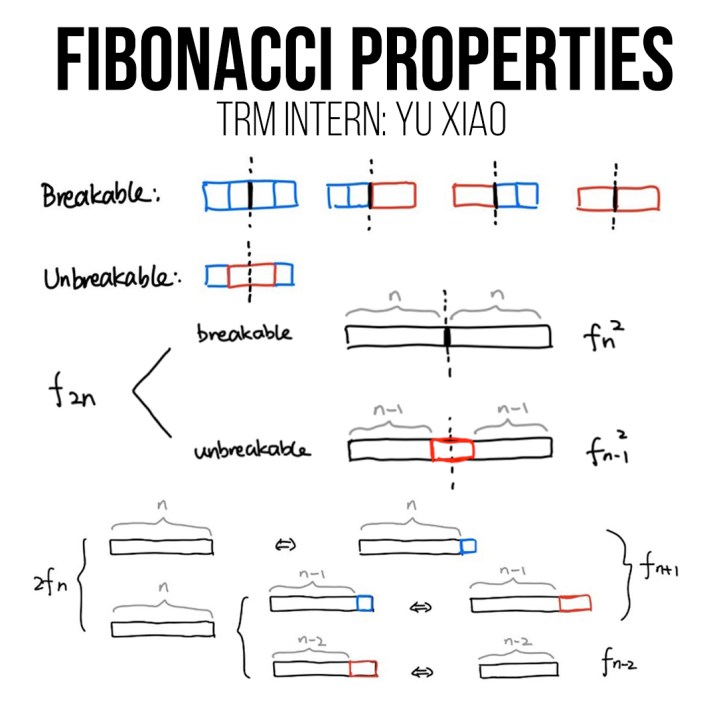
Yu Xiao – Visual Proofs of Fibonacci Properties
Yu Xiao – Maths Proofs Without Words

Akis Androulakis – Gambling and the Law of Large Numbers

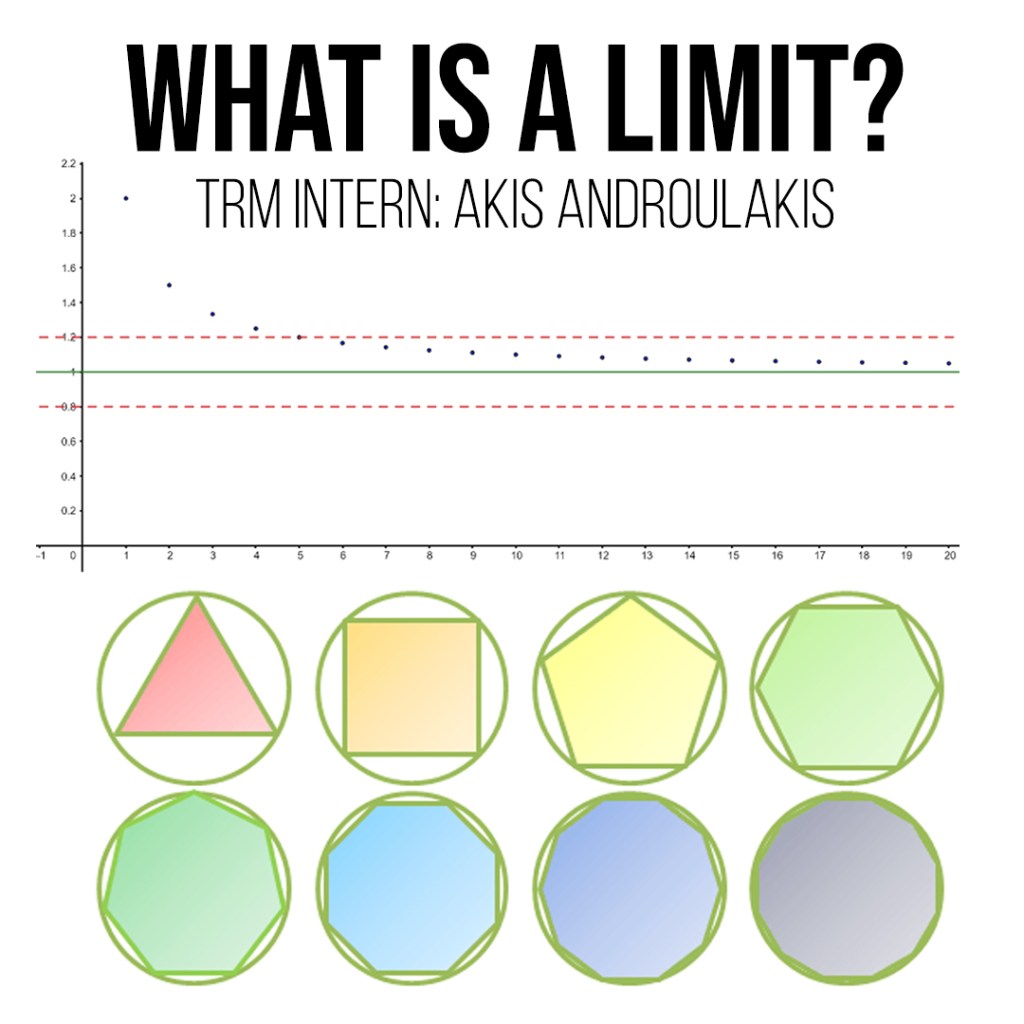
Akis Androulakis – Puzzling Limits

Akis Androulakis: The Mathematical Definition of a Limit
Aryaman Gupta – Mathematical Philosophy: Russell, Godel and Incompleteness

Aryaman Gupta – Mathematical Philosophy: The Decidability Problem

Aryaman Gupta: An Introduction to Maths and Philosophy – Platonism, Formalism and Intuitionism

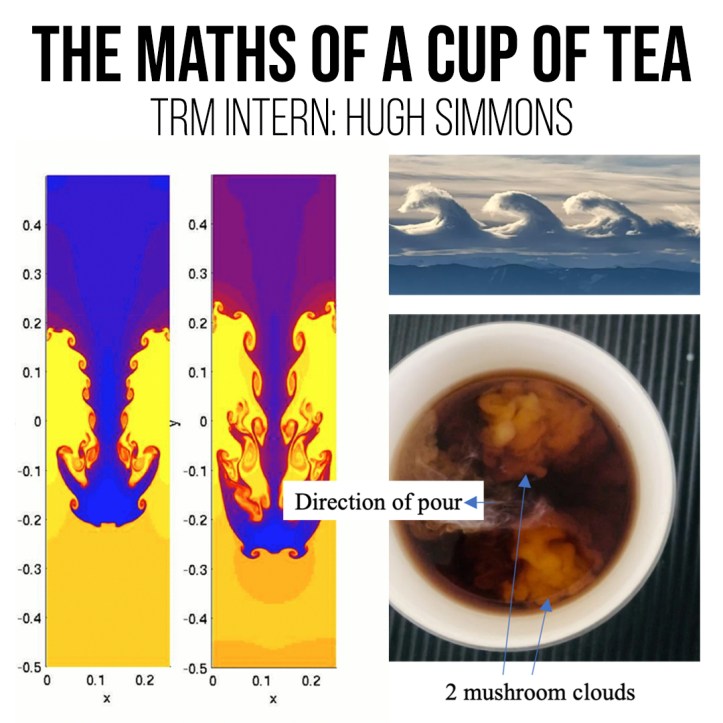
Hugh Simmons – The Maths of a Cup of Tea
Chenying Liu – Tom and Jerry: the never-ending game of Chase and Escape (Part 2)

Chenying Liu – Tom and Jerry: the never-ending game of Chase and Escape (Part 1)

Agnieszka Wierzchucka – The Quest to Heisenberg’s Uncertainty Principle: Part III

Agnieszka Wierzchucka – The Quest to Heisenberg’s Uncertainty Principle: Part II

Agnieszka Wierzchucka – The Quest to Heisenberg’s Uncertainty Principle: Part I

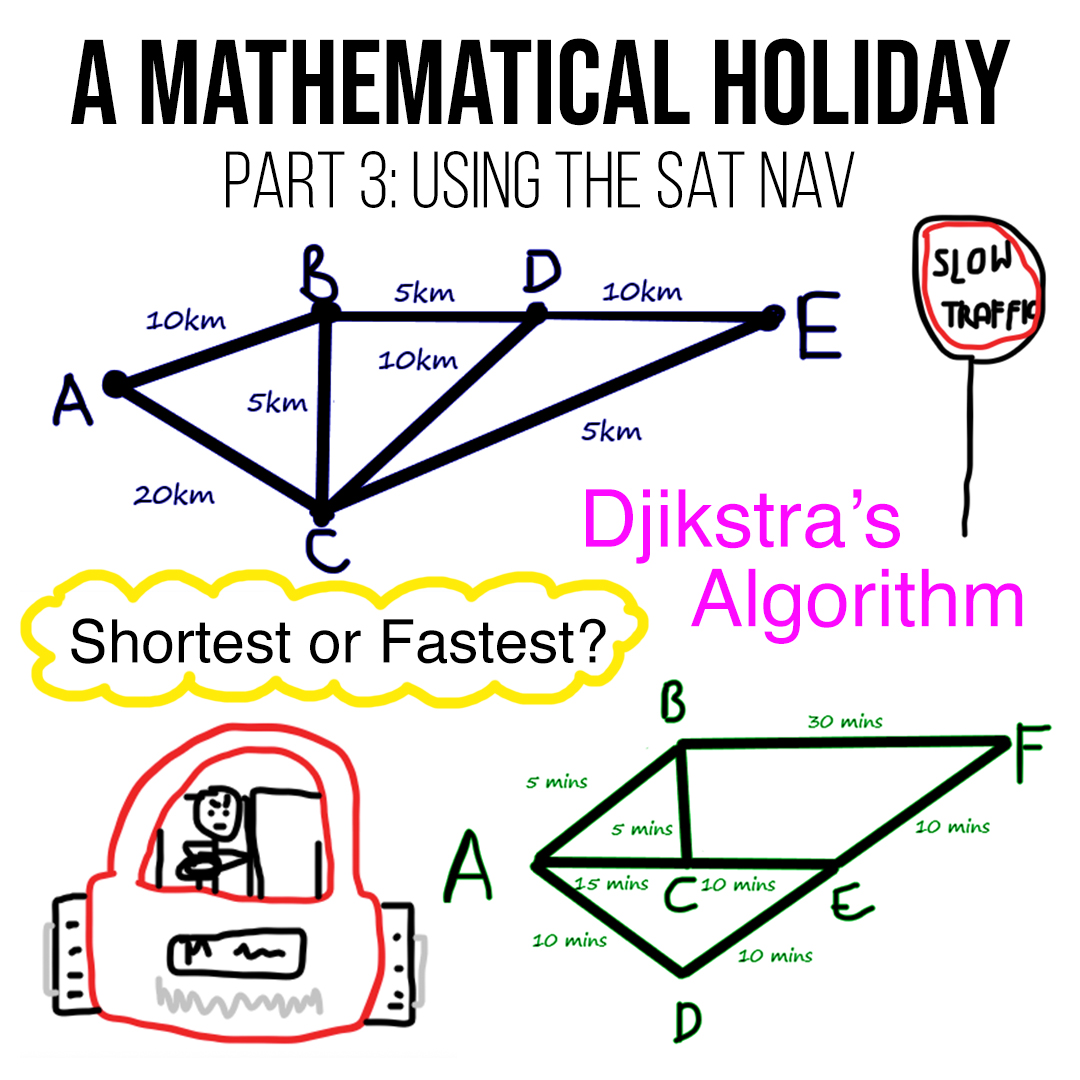
Molly Roberts – A Mathematical Holiday (Part 3): Using the Sat Nav
Molly Roberts – A Mathematical Holiday (Part 2): Sorting the Luggage

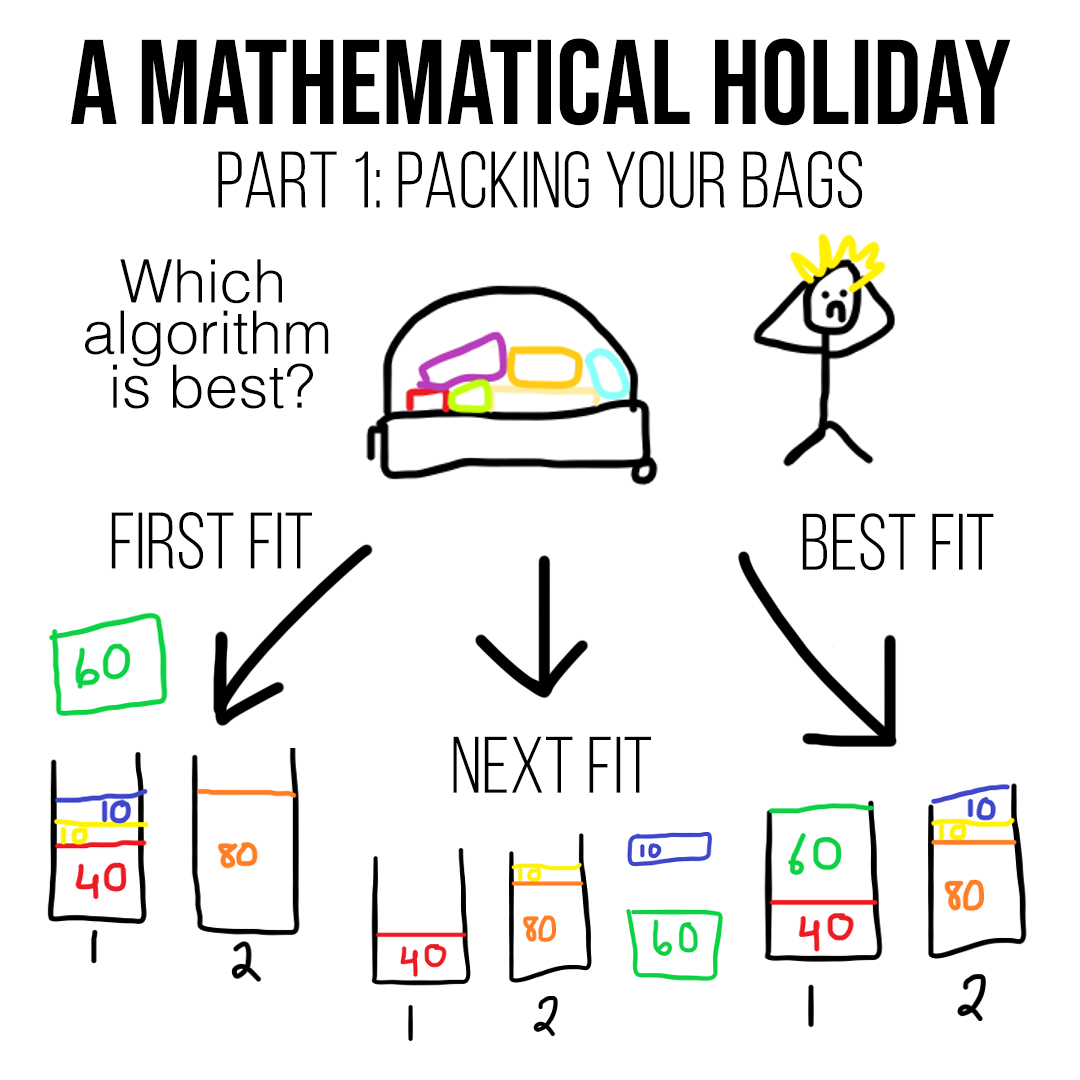
Molly Roberts – A Mathematical Holiday (Part 1): Packing Your Bags
Molly Roberts – Numbers with Cool Names: Weird, Sexy and Untouchable

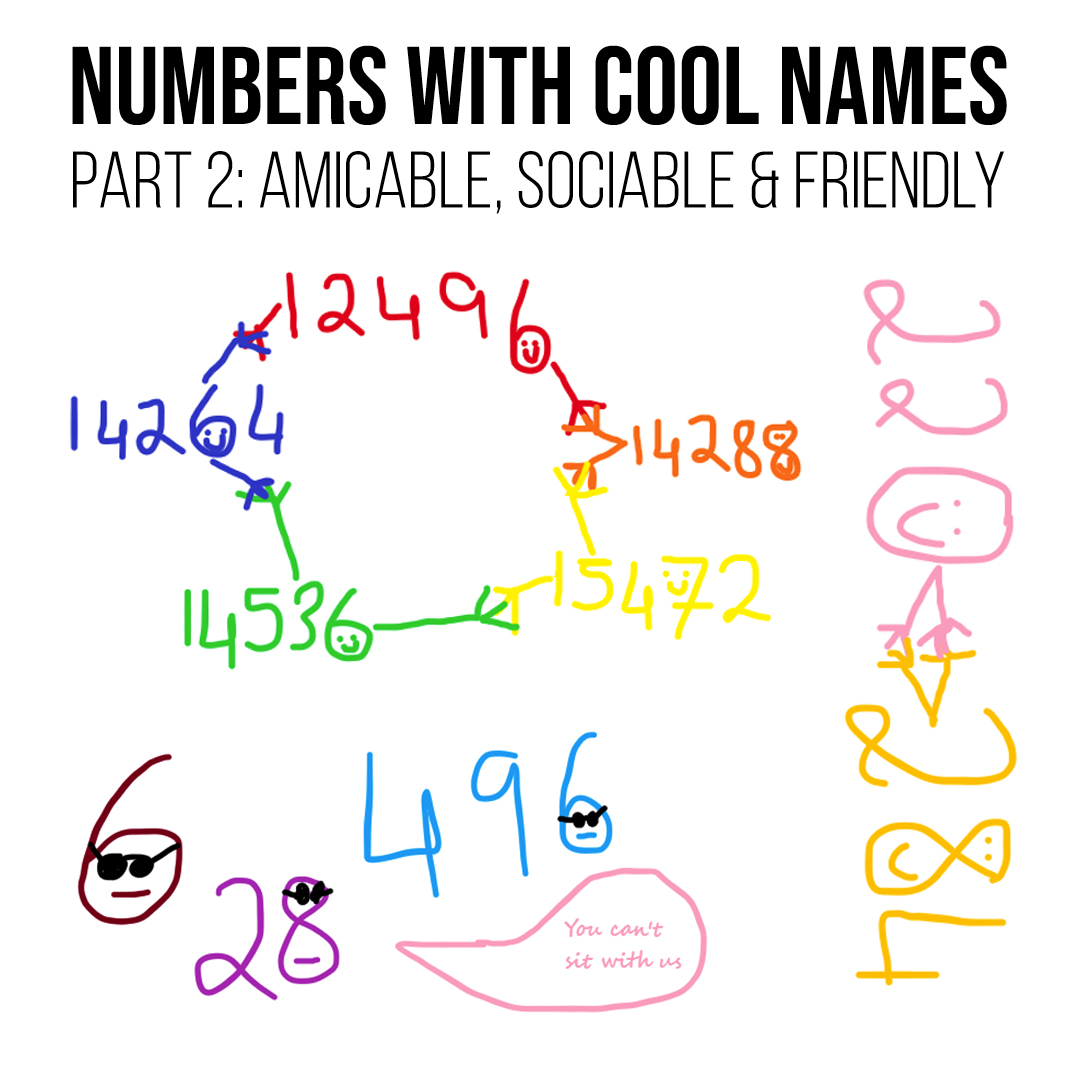
Molly Roberts – Numbers with Cool Names: Amicable, Sociable, Friendly
Molly Roberts – Numbers with Cool Names: Happy, Lucky and Perfect

Khanh Giang – Why don’t we have Quantum Computers already?

Khanh Giang – How do we build a Quantum Computer?

Khanh Giang – Why do we need Quantum Computers?

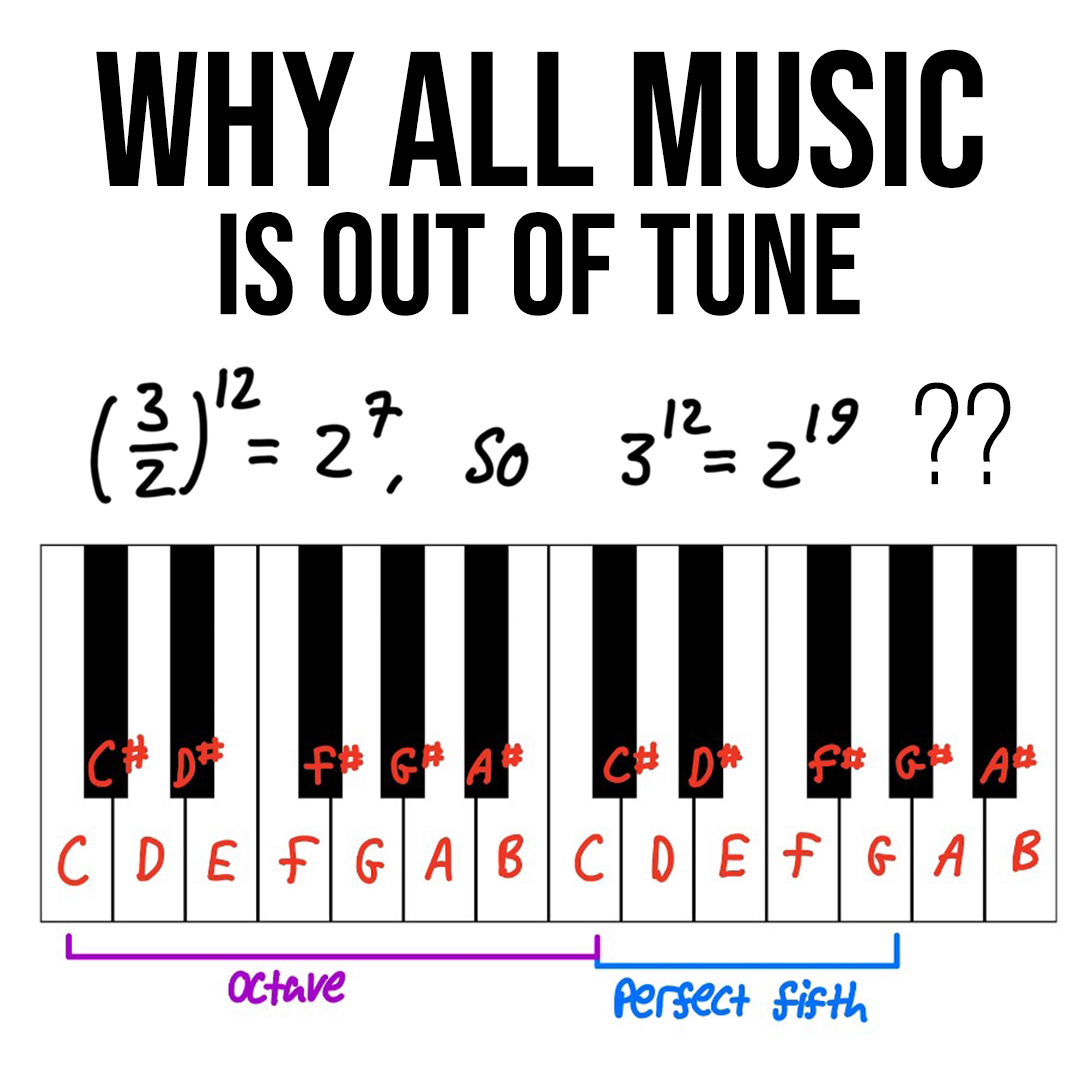
Aidan Strong – Why all music is out of tune
Aidan Strong – Why all World Maps are Wrong

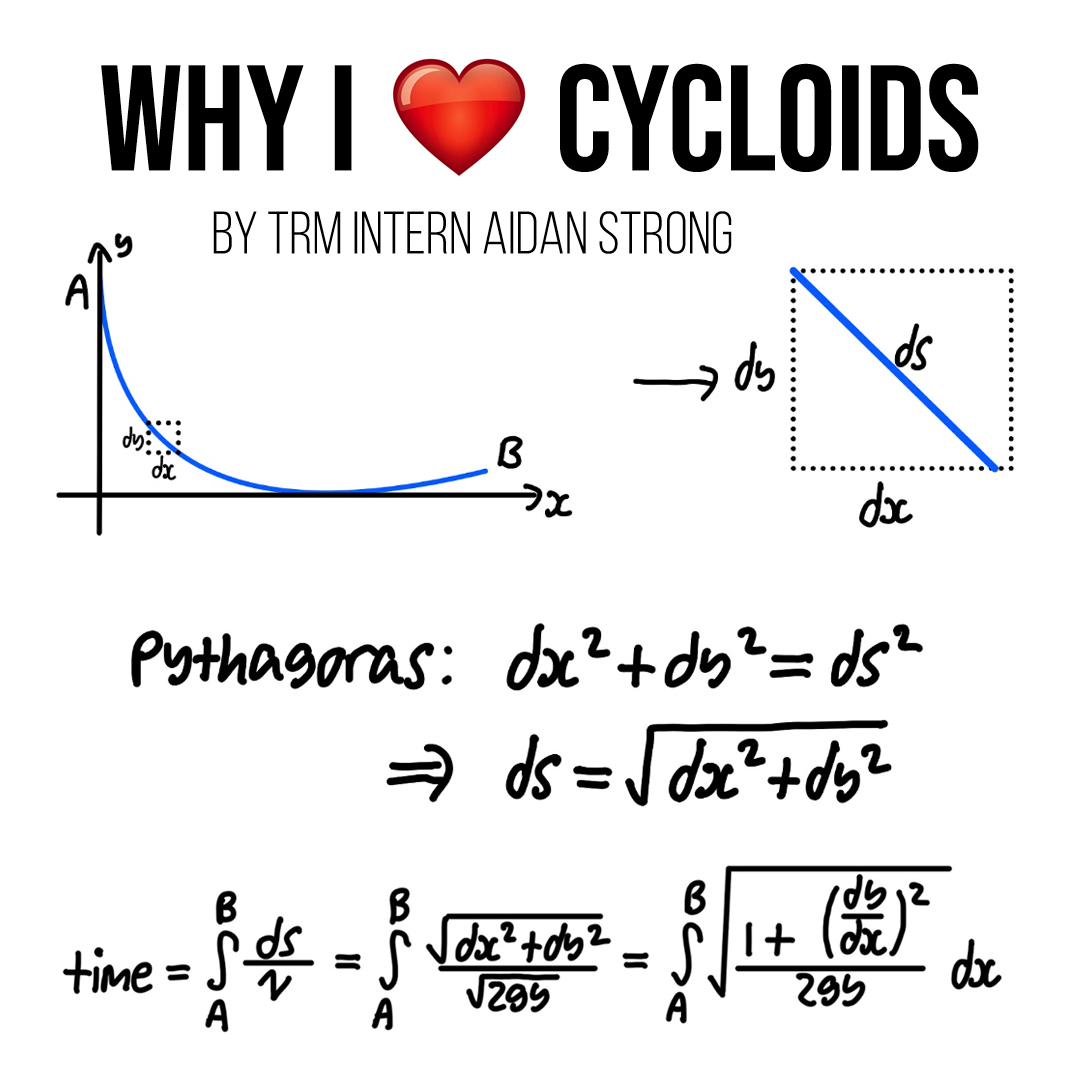
Aidan Strong – Why the Cycloid is the best curve
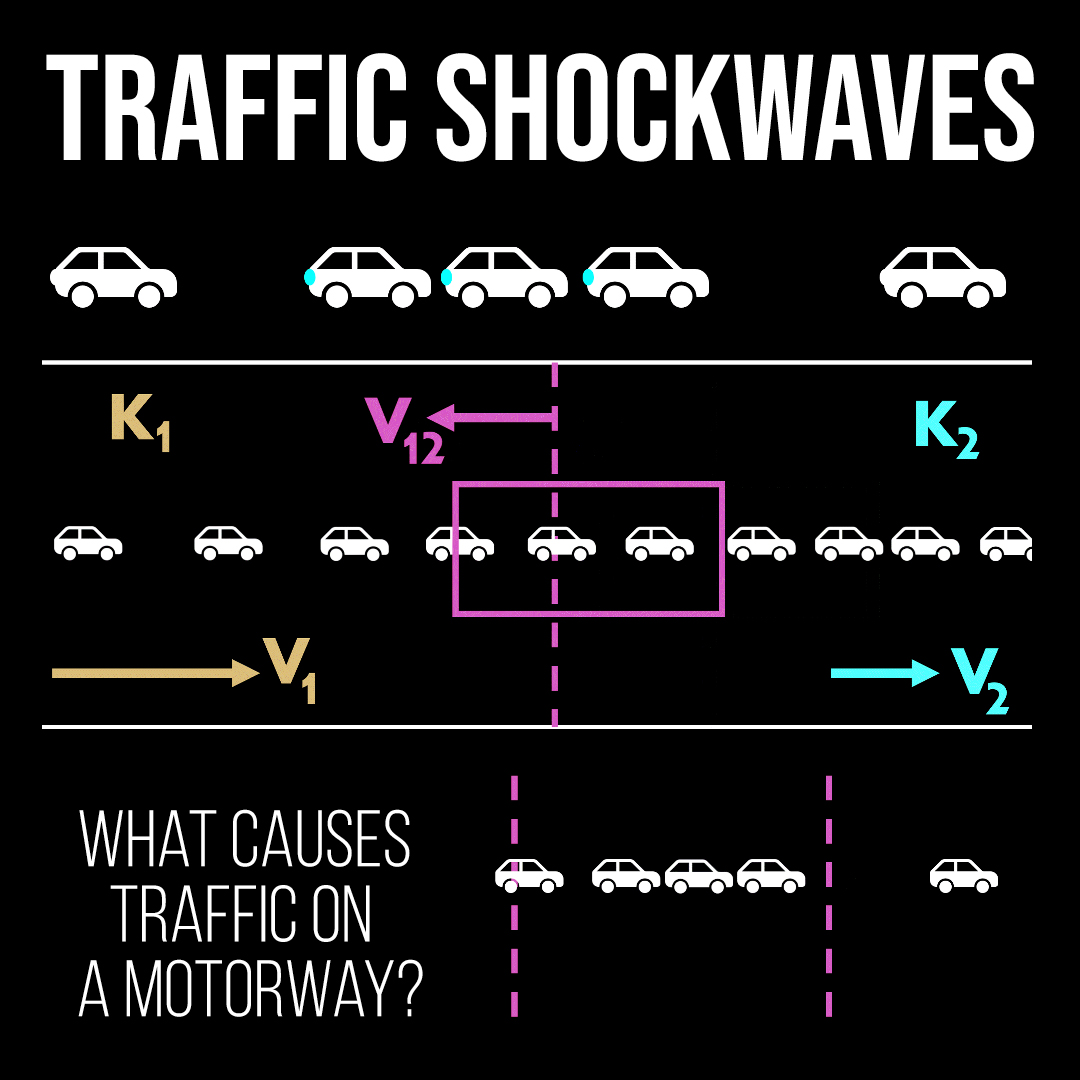
Ifan Rogers – Traffic Shock Waves
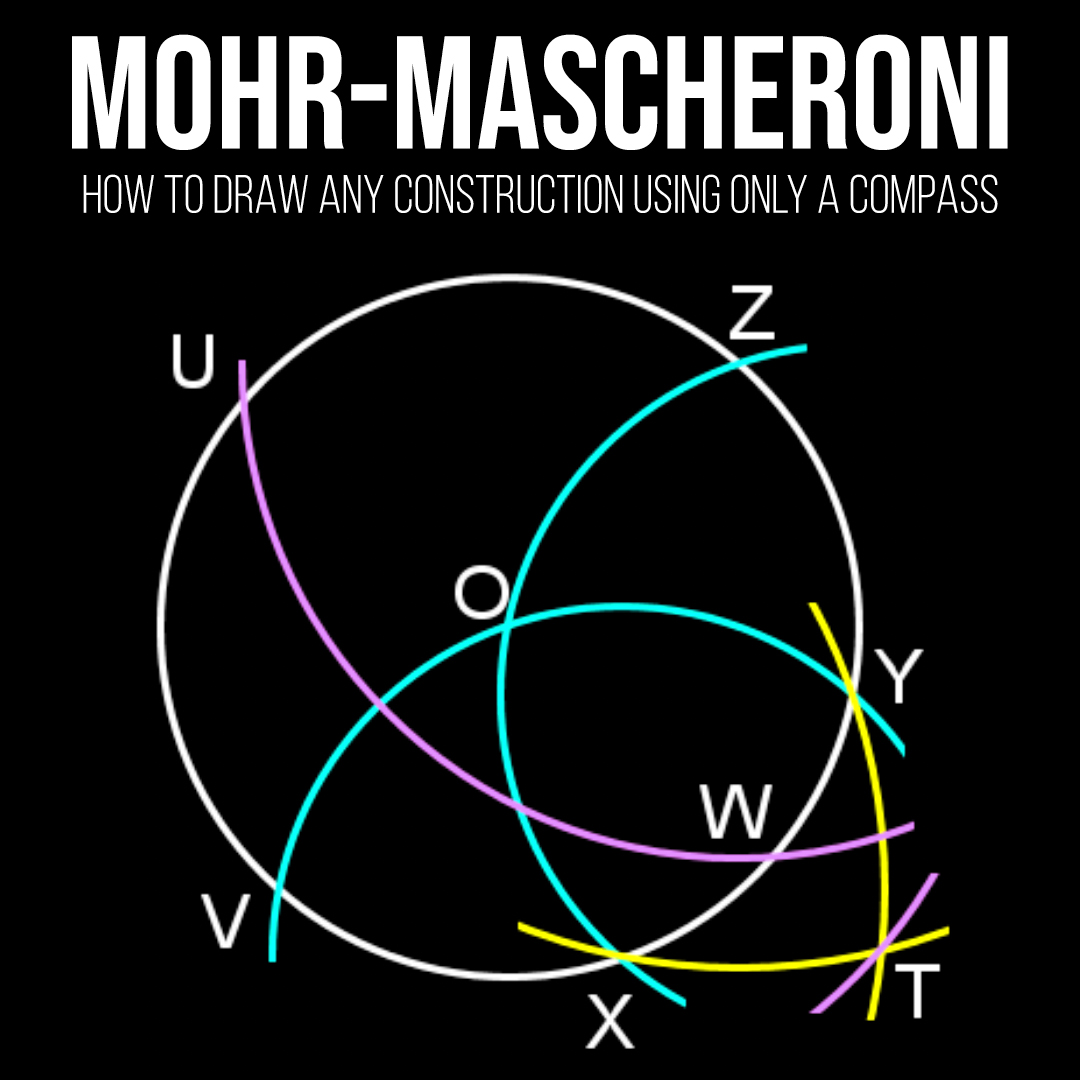
Ioana Bouros: Mohr-Mascheroni Theorem
Ioana Bouros: Mendelian Genetics

Ioana Bouros: Small World Effect

Ioana Bouros: Frieze Patterns at the Ashmolean Museum

Ioana Bouros: Wallpaper Groups and Tiling Floors

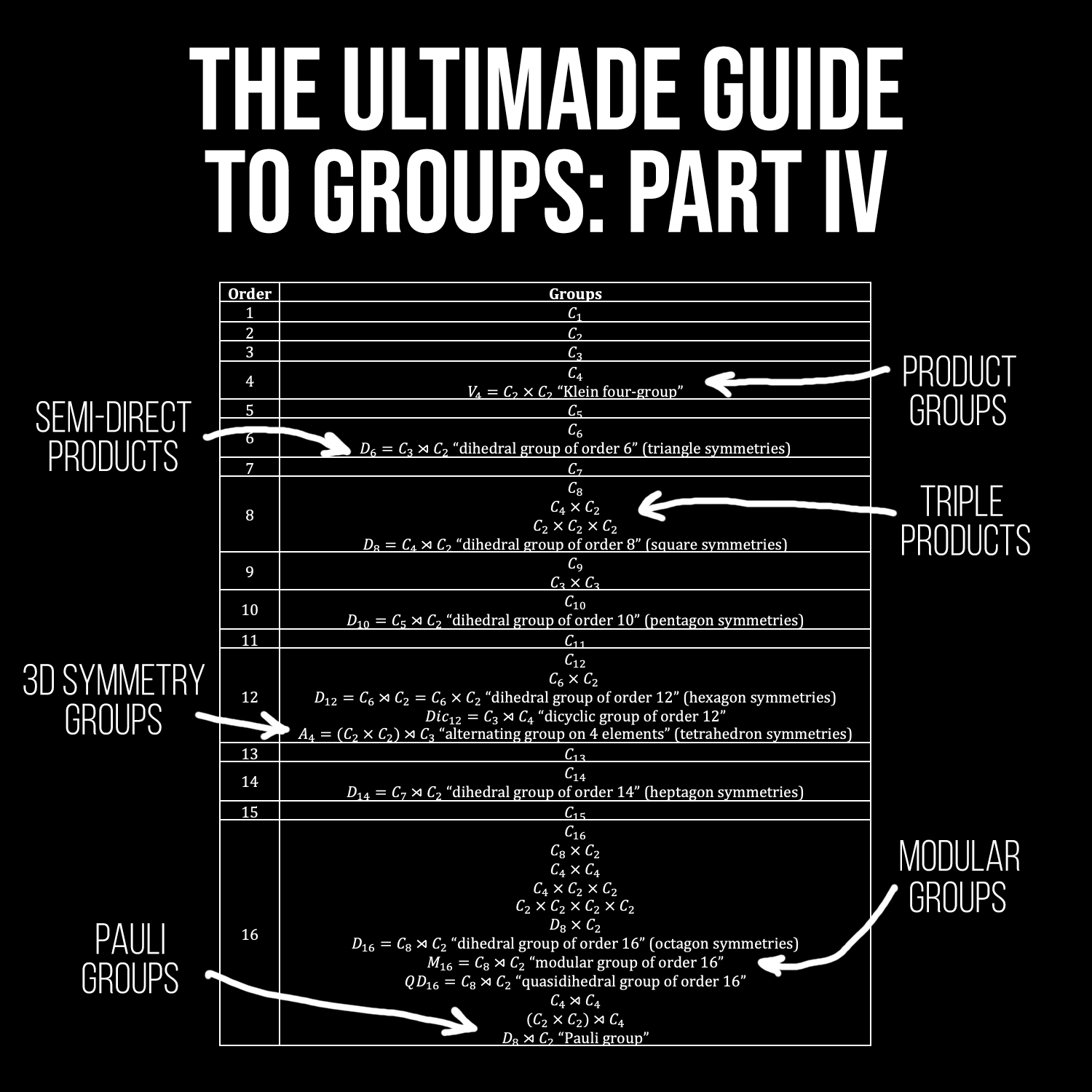
Gavin Bala: The Ultimate Guide to Groups: Part IV
Semu Serunjogi – From Handshakes to Mountains via Bijections

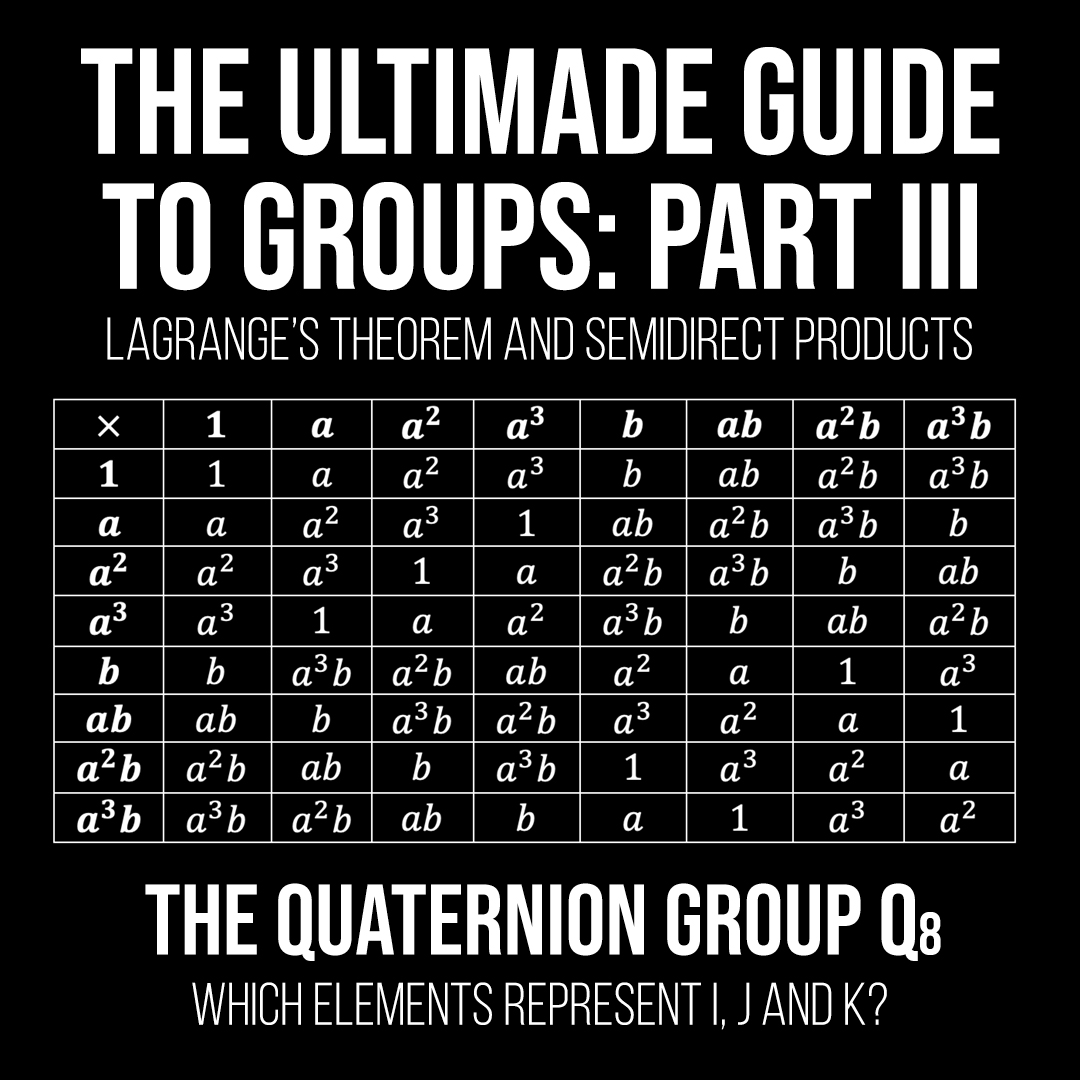
Gavin Bala – The Ultimate Guide to Groups: Part III
Semu Serunjogi – Counting Mountain Ranges

Gavin Bala – The Ultimate Guide to Groups: Part II

Semu Serunjogi – Counting Socially Distanced Handshakes

Gavin Bala – The Ultimate Guide to Groups: Part I

Semu Serunjogi – Catalan Numbers: An Introduction to Recurrence Relations

Gavin Bala – The 9 Regular Polyhedra

The Finite Calculus: Part II Integration

Gavin Bala – The Finite Calculus Part I

Gavin Bala – How to Build a Settlement on Mercury with the Heat Equation

Gavin Bala – The Heat Equation and Wine Cellars

Lorenzo Piersante – How do computers simulate the real world?

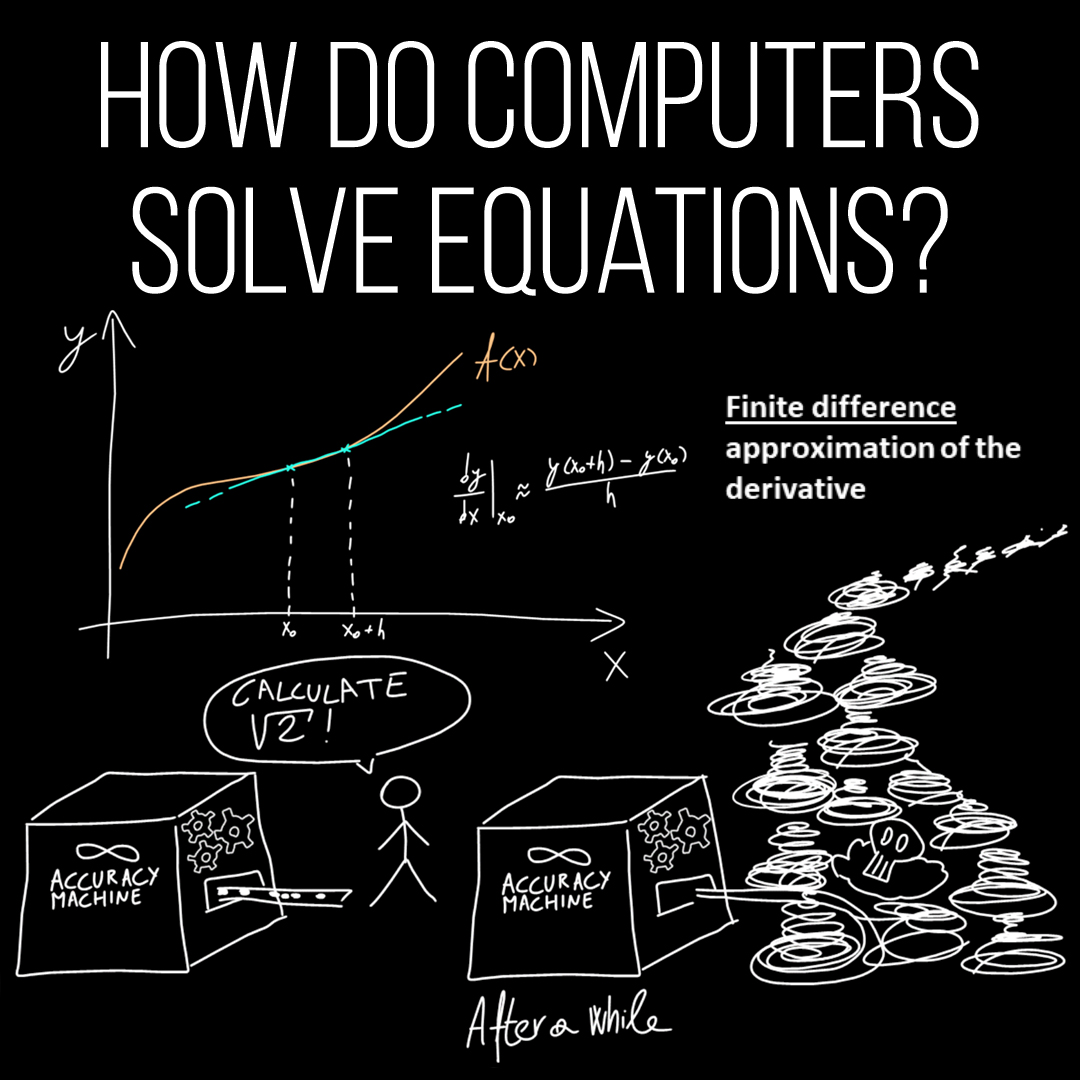
Lorenzo Piersante – How do computers solve equations?
Lorenzo Piersante – How do Computers do Maths?

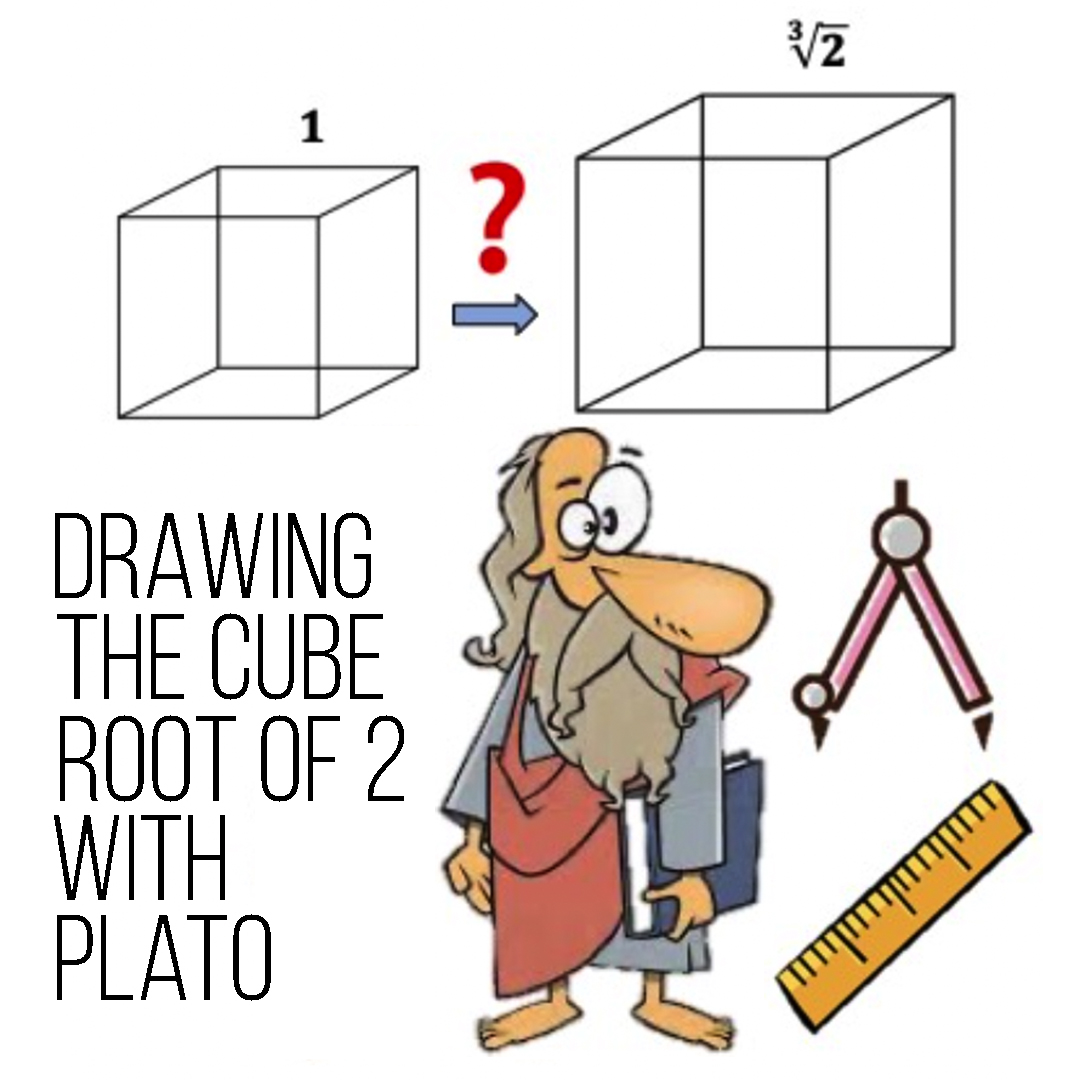
Chenying Liu – Drawing the Cube Root of 2 with Plato
Chenying Liu – Give Me Paper and I Shall Fold the Cube Root of 2

Chenying Liu – Creating the Cube Root of 2: From Apollo to Plato

Siddiq Islam – Is Visual Mathematics Artistic?
Siddiq Islam – Is Visual Art Mathematical?
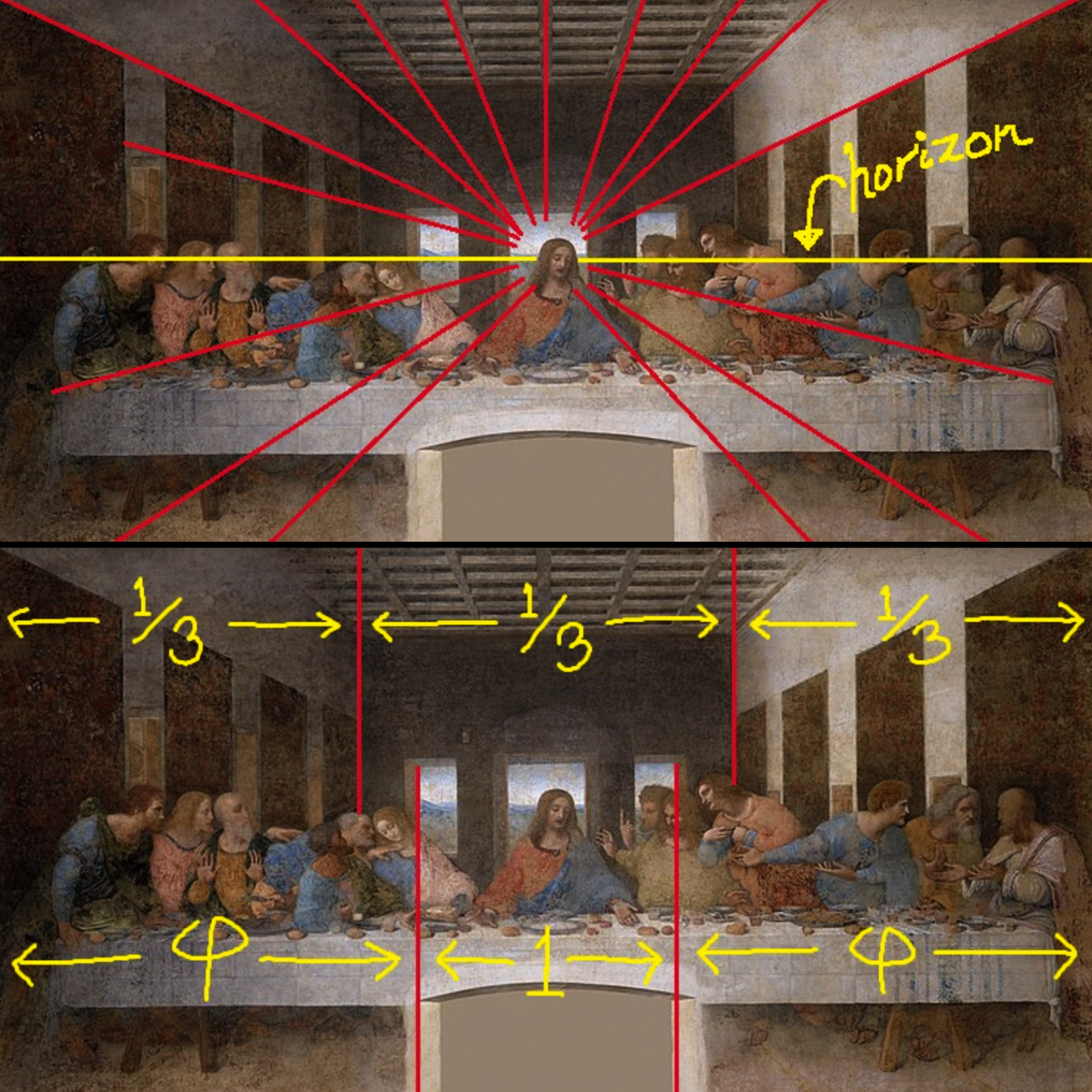
Vlad Bercovici – Mathematically Proving Why You Should Avoid Las Vegas (Part 3 of 3)

Vlad Bercovici – Linear recurrence relations and how to solve them (Part 2 of 3)

Vlad Bercovici – Probability is everywhere. But what is it exactly? (Part 1 of 3)

Wilf Offord – Quantum Teleportation and Entanglement: How do they work?

Wilf Offord – 5 Types of Infinity
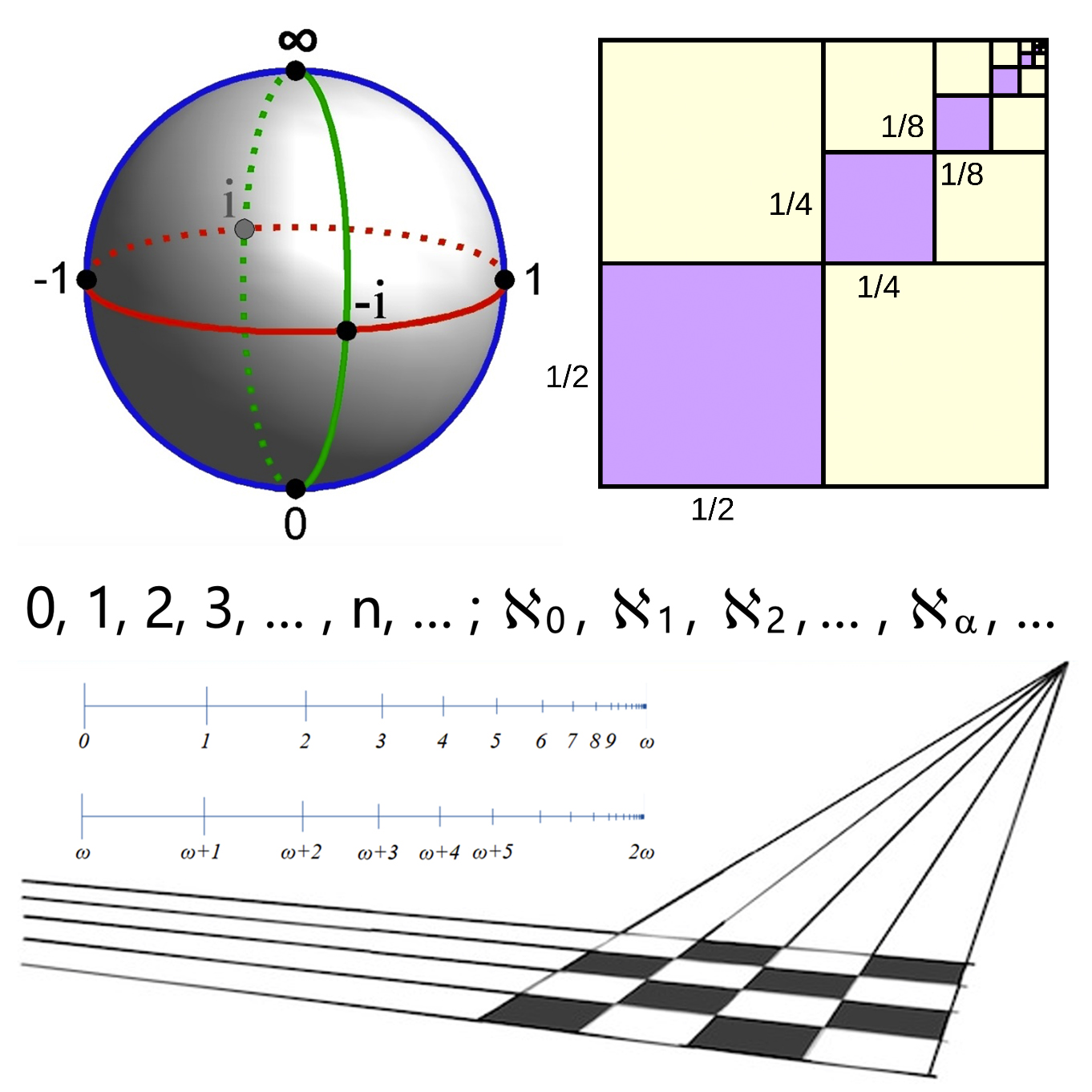
Wilf Offord – How Quantum Computers Work (and why you should care)

Becca Tanner – Fermi Problems Part 3: Where is everybody?
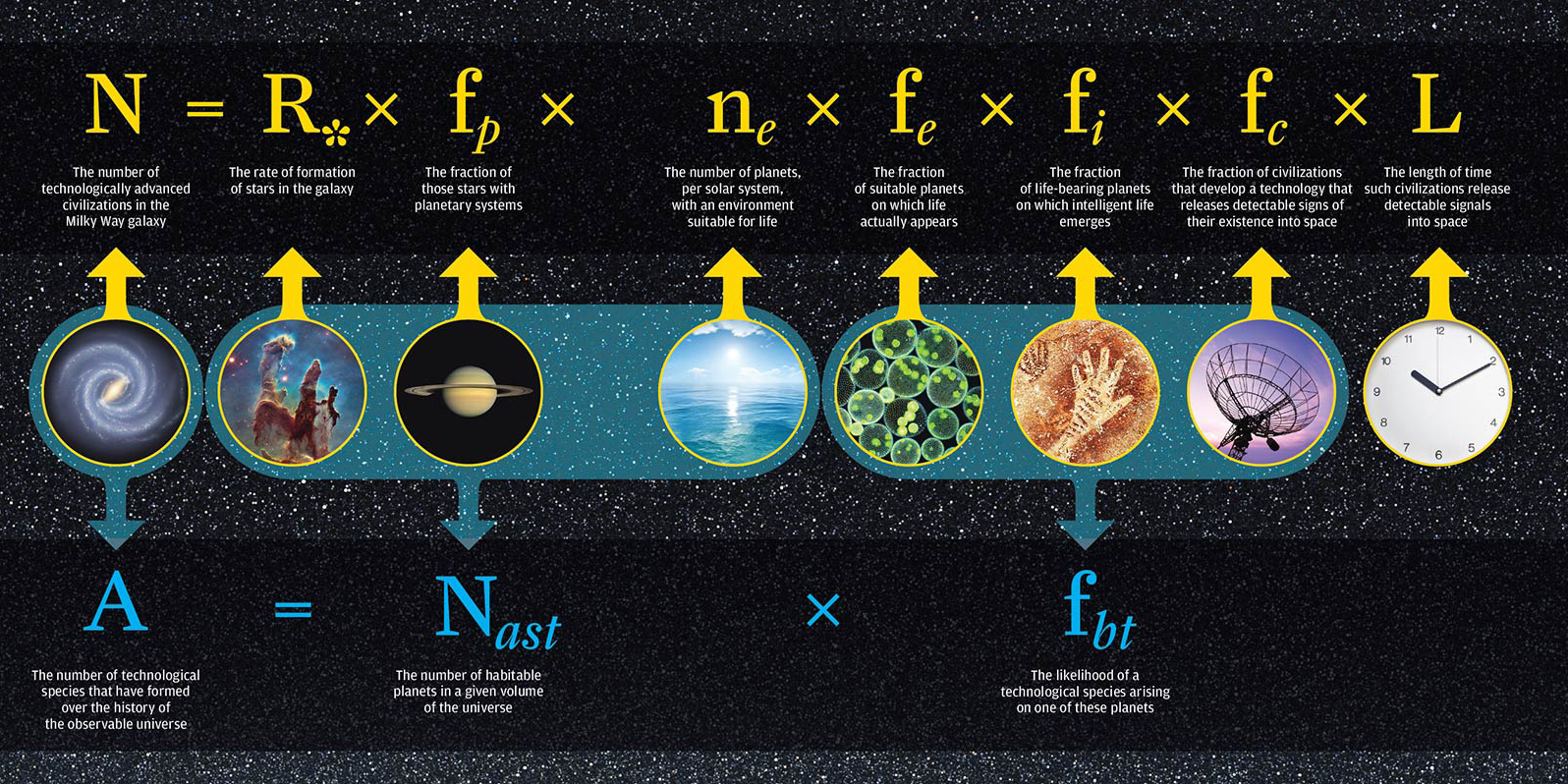
Becca Tanner – Fermi Problems Part 2: Don’t sweat the small stuff
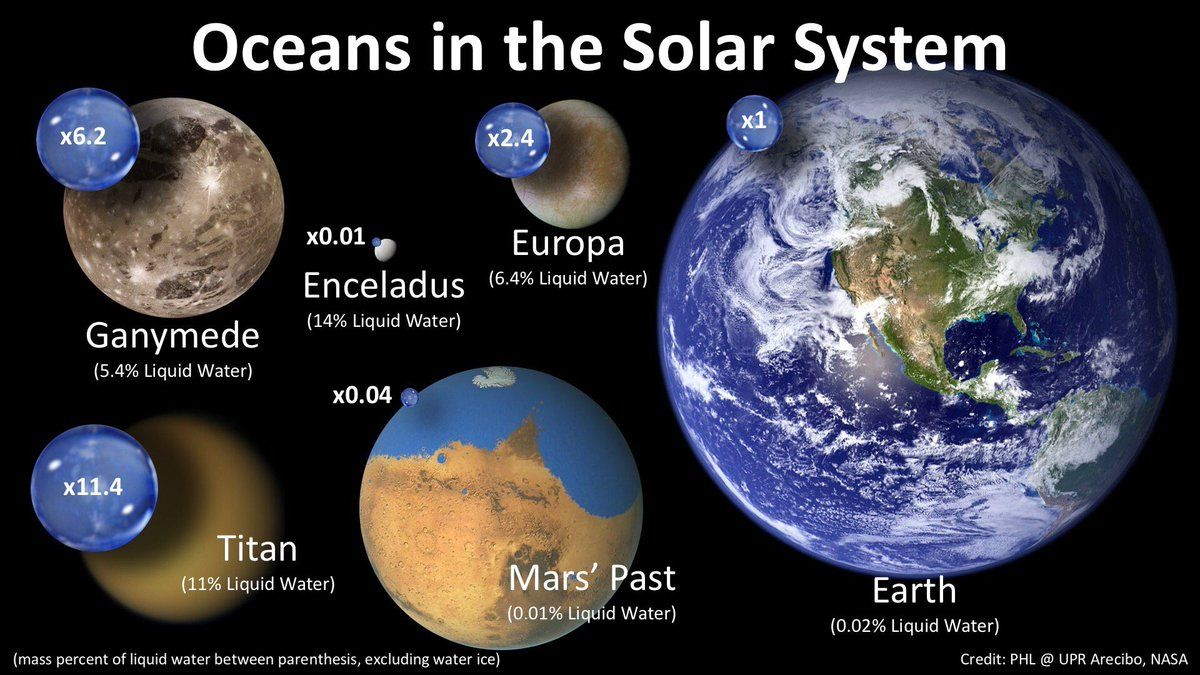
Charlie Ahrendts – Stop 5: Planet of Continuity
Charlie Ahrendts – Stop 4: Realm of Chaos

Charlie Ahrendts – Stop 3: Multi-dimensional World

Charlie Ahrendts – Stop 2: Fluid Planet
Charlie Ahrendts – Stop 1: Positivity Planet
Charlie Ahrendts – Gödels Incompleteness Theorem Explainer

Charlie Ahrendts – Set Theory Explainer

Charlie Ahrendts – Axioms of the Real Numbers Explainer

Charlie Ahrendts – Journeying Across the Mathematical Universe

Alex Nikic – Testing for Divisibility of ANY Number

Becca Tanner – Fermi Problems Part 1: Envelopes at the Ready!

Sam Flower – Level 3: Doughnuts all the way down
Sam Flower – Level 2: Houston, we have a problem

Iain Duncan – How fast does Santa travel?

Iain Duncan – The Maths of Santa Claus

Sam Flower – Level 1: Space is a Doughnut

Sam Flower – Maths of the Pokédex

Amie Campbell – Comparing Disease Tests using ROC Curves and AUC Values

Amie Campbell – Sensitivity, Specificity and Confusion Matrices

Sian Langham – The Maths of Poker

Sian Langham – Catching Fraudsters with Maths

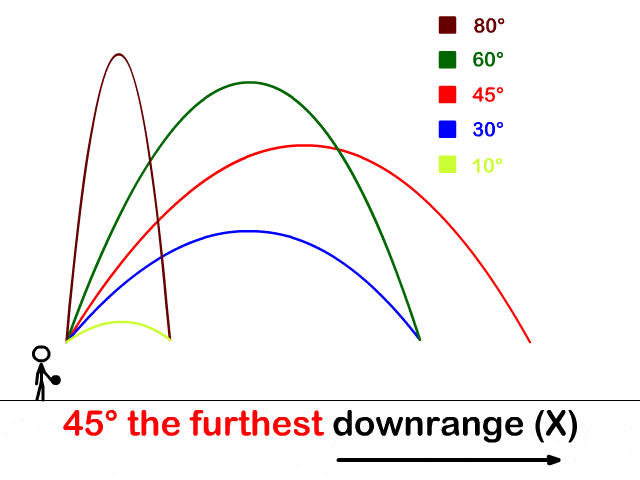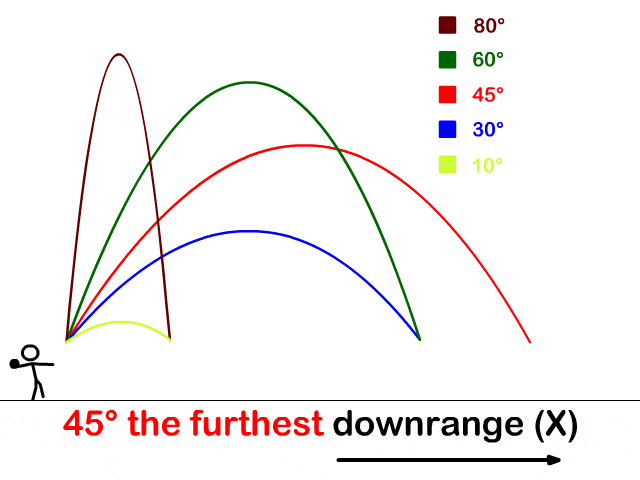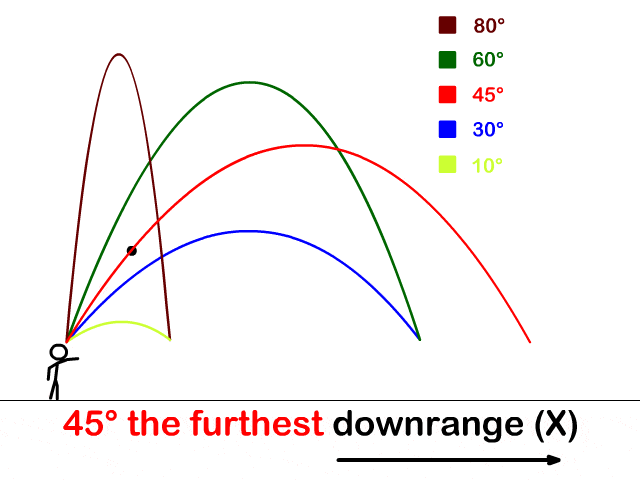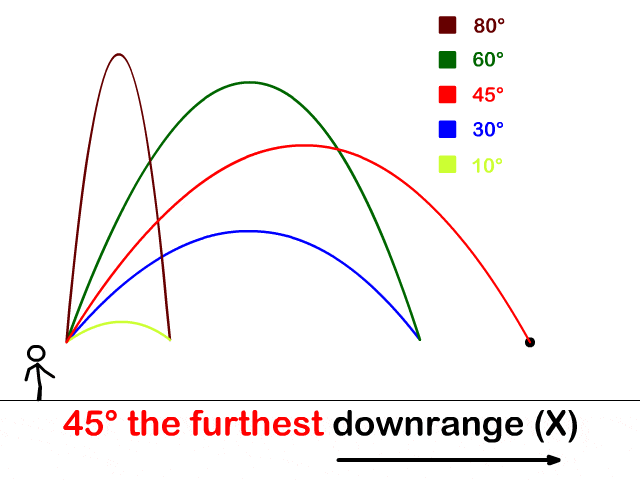
Sian Langham – Golf and Projectile Motion

Sian Langham – Binary Code and Storing Music on Computers

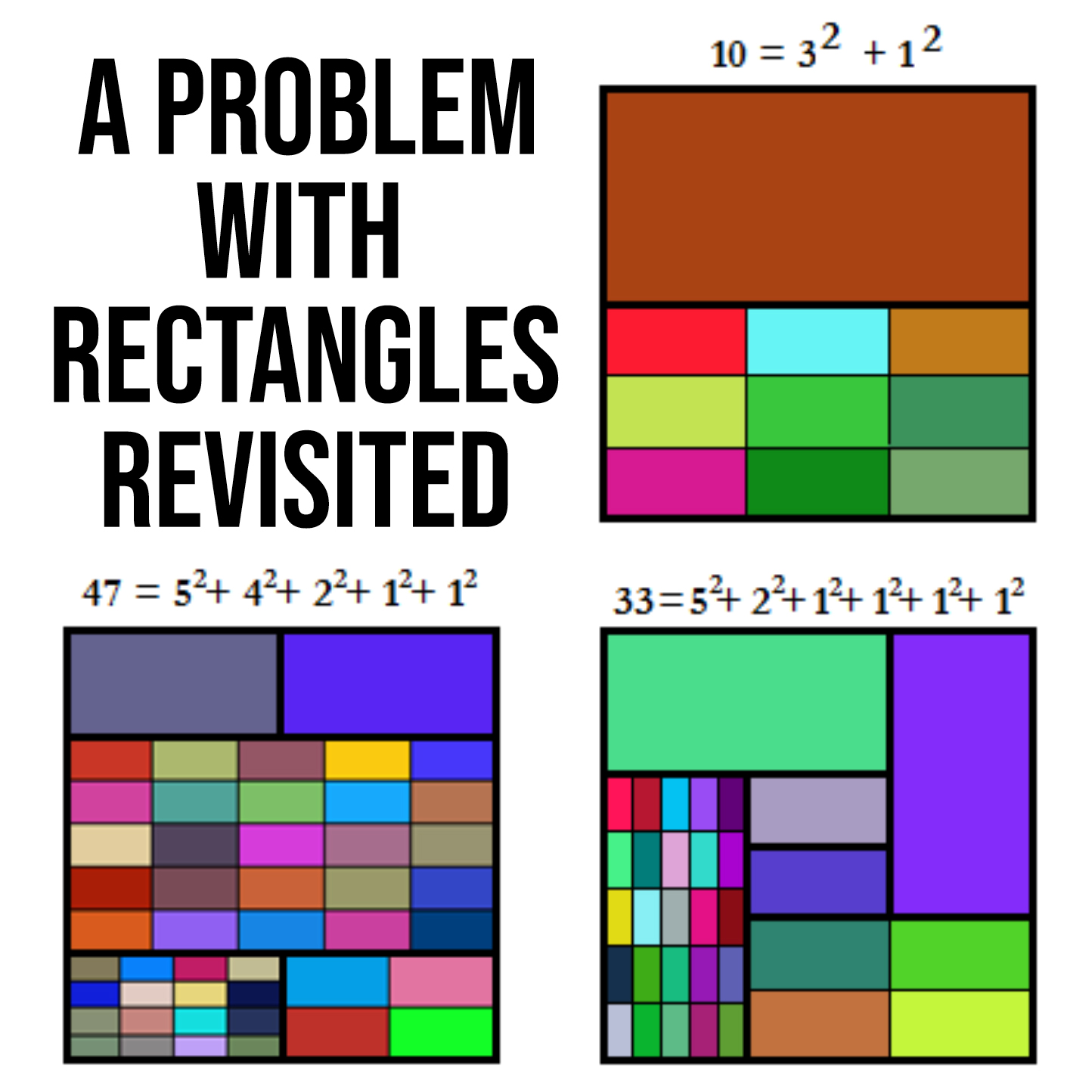
Lewis Baxter – A Problem with Rectangles Revisited
Justin Leung – Complex Numbers, Air Traffic Control and RADAR
Justin Leung – Mathsquake: the Maths of Earthquakes
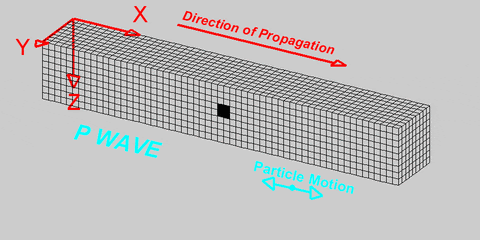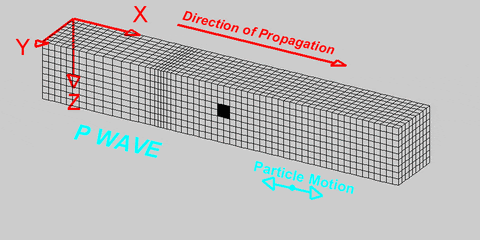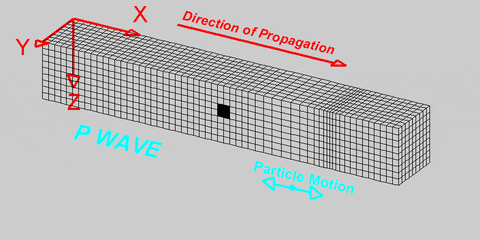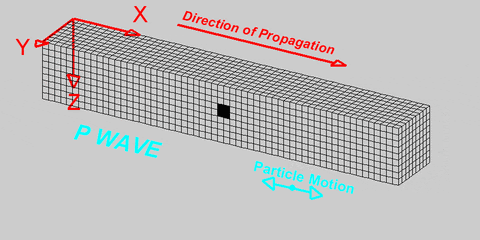
Ruby Nixson – The Normal Distribution and the Central Limit Theorem



Megan Bell: The Prosecutor’s Fallacy

Megan Bell: Bayes’ Theorem and Disease Testing

Megan Bell: Ghosts, Spam Emails and Bayes’ Theorem

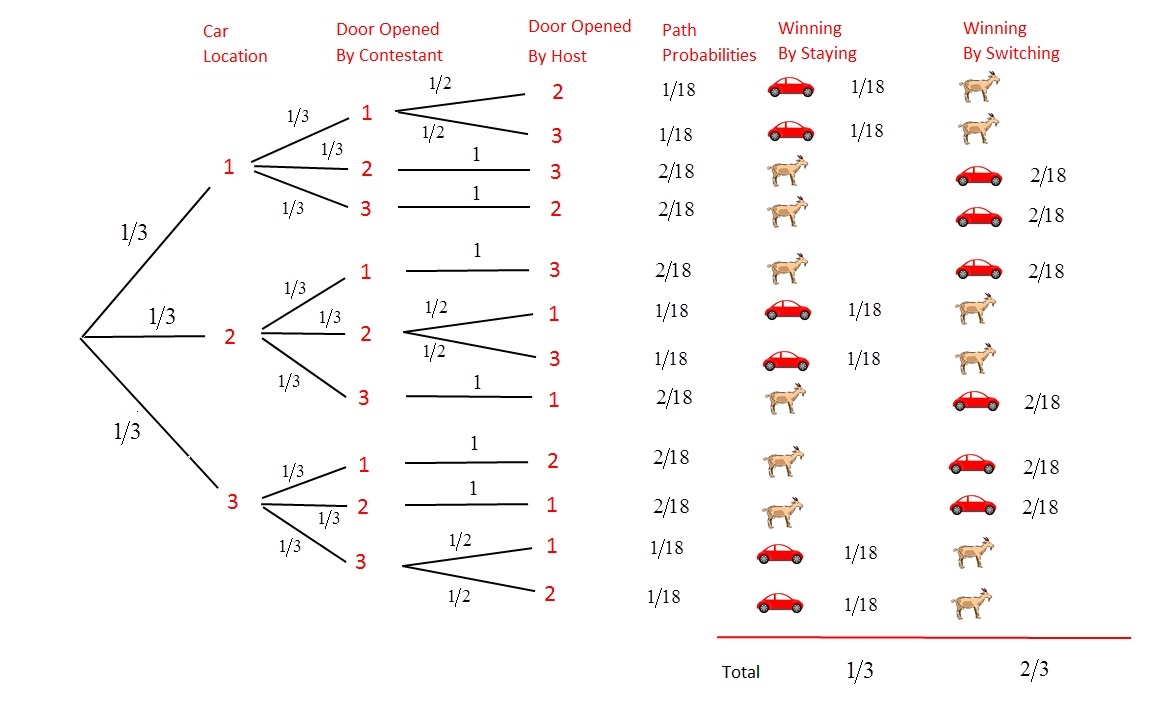
Jakub Michalski – The Problem with Monty Hall
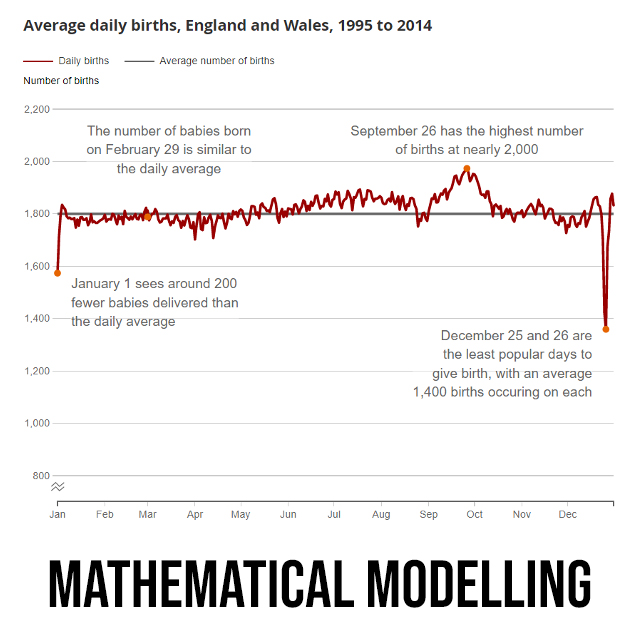
Jakub Michalski – Mathematical Modelling: Earthquakes, Coin Flips and Birthdays
Jakub Michalski: Bertrand Paradox
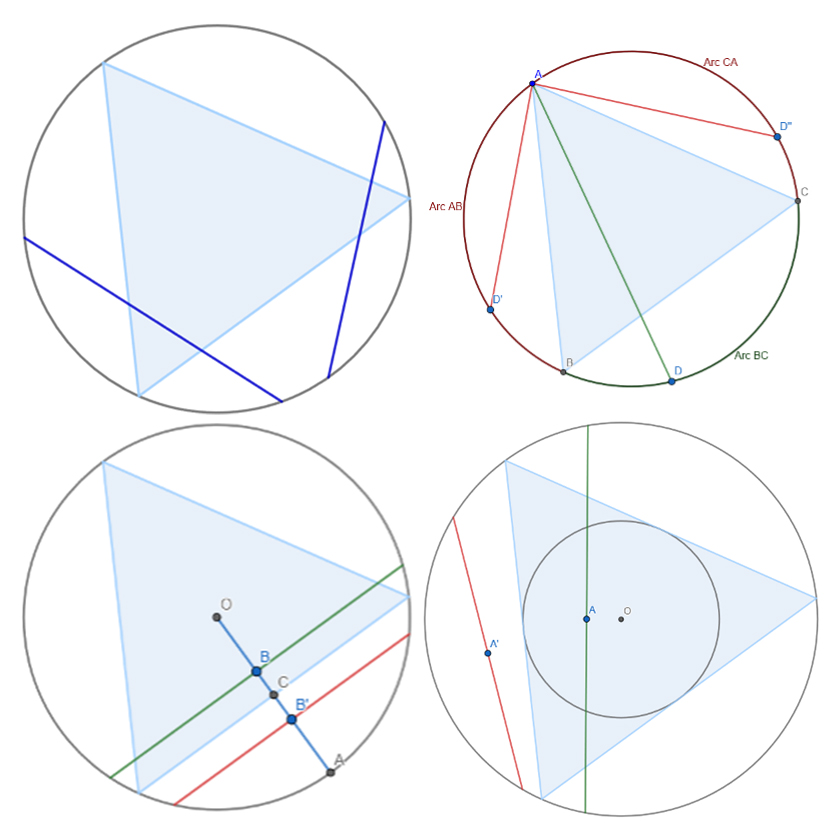
Georgie Bumpus: Elliptic Curve Cryptography

Georgie Bumpus: RSA Cryptography

Georgie Bumpus: Substitution Ciphers


Lynn Gui: Why e deserves the name ‘natural base’
Lynn Gui: e and the Sheldon Mitosis

Alex Homer: Monty Hall Origins

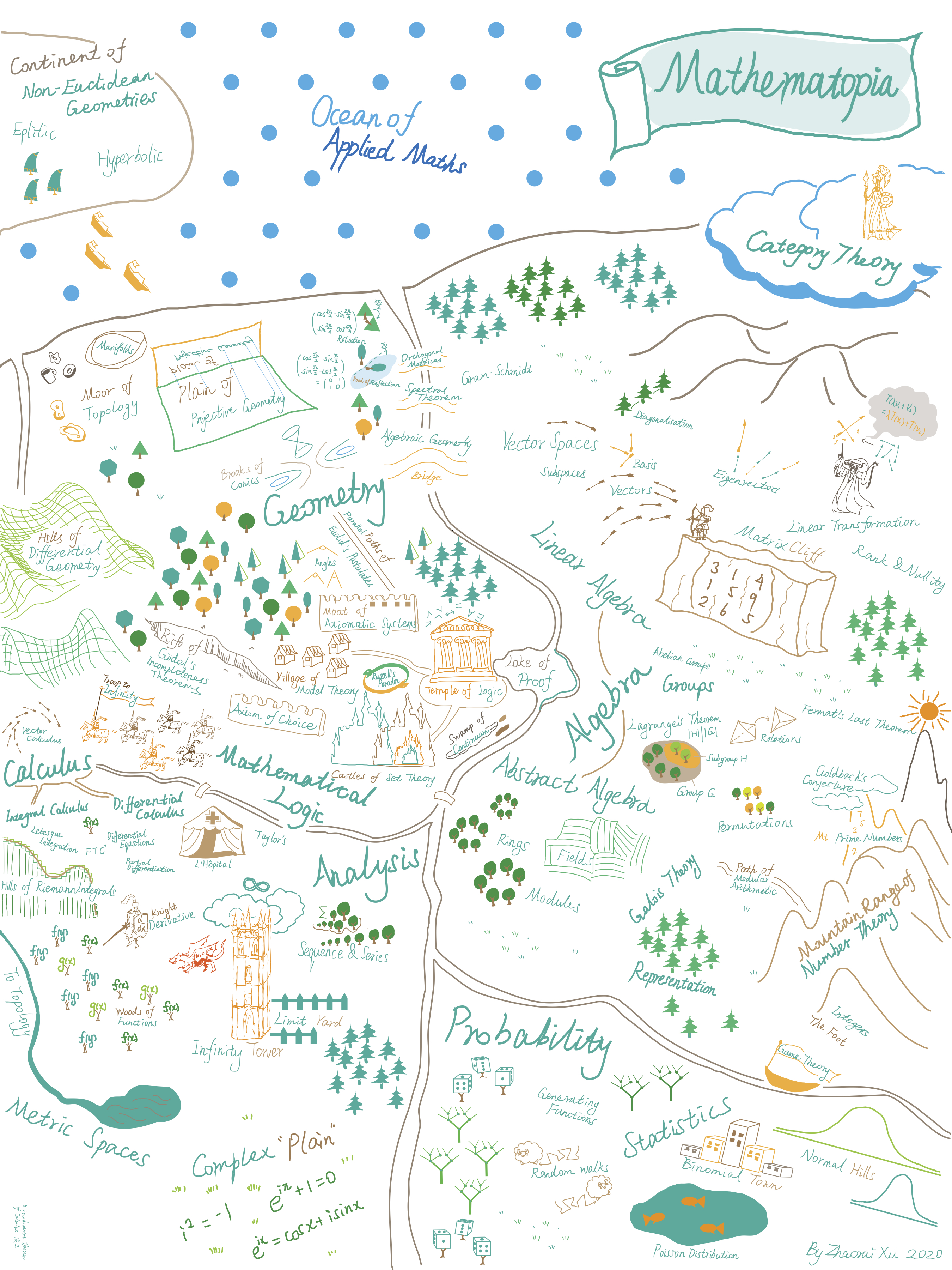
Zhaorui Xu – The Adventurer’s Guide to Mathematopia: Part 3
Alex Homer: Monty Hall Extended

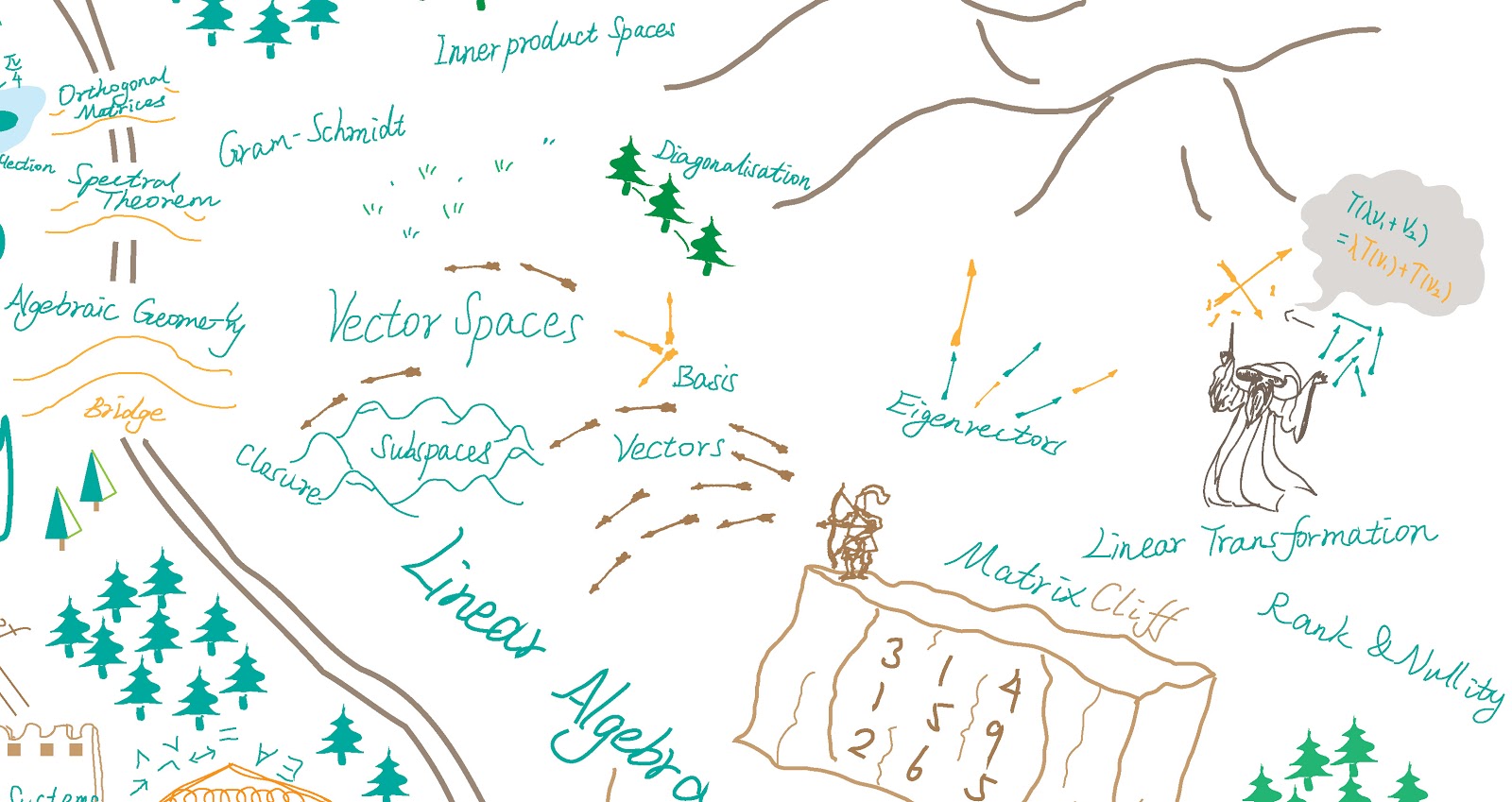
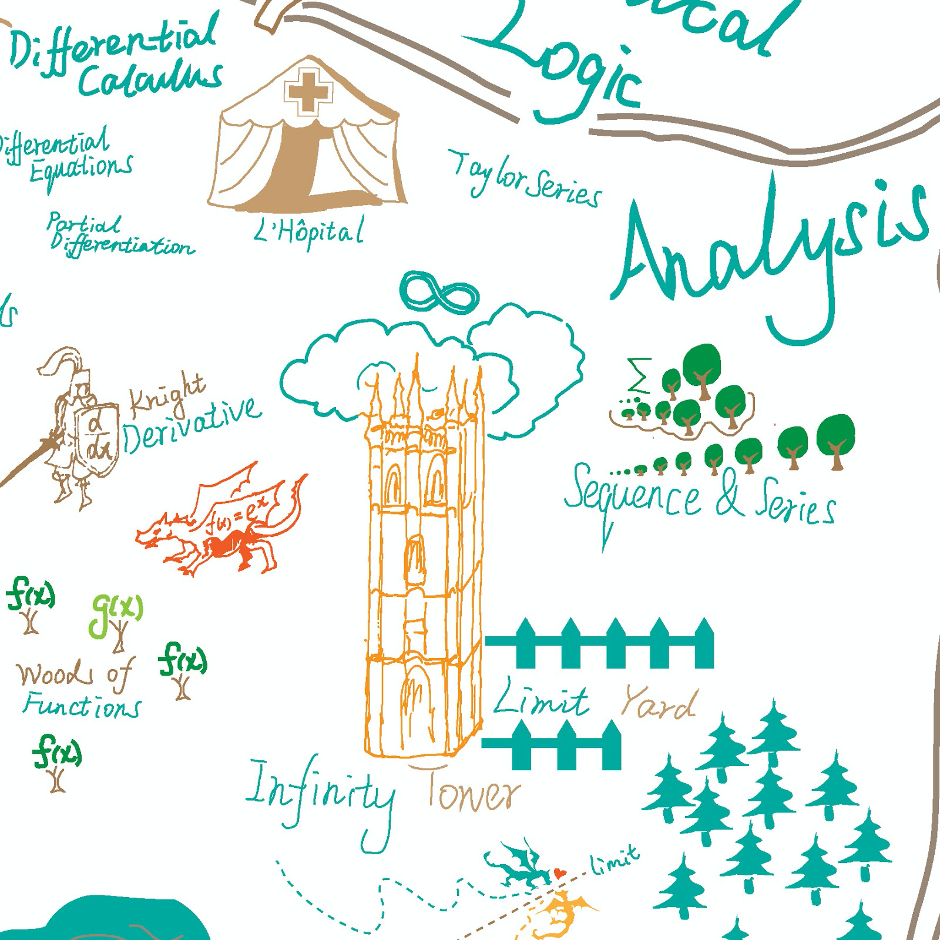
Zhaorui Xu – The Adventurer’s Guide to Mathematopia: Part 2
Alex Homer: Monty Hall Revisited

Zhaorui Xu – The Adventurer’s Guide to Mathematopia: Part 1
Zhaorui Xu: Mathematopia – The Adventure Map of Mathematics
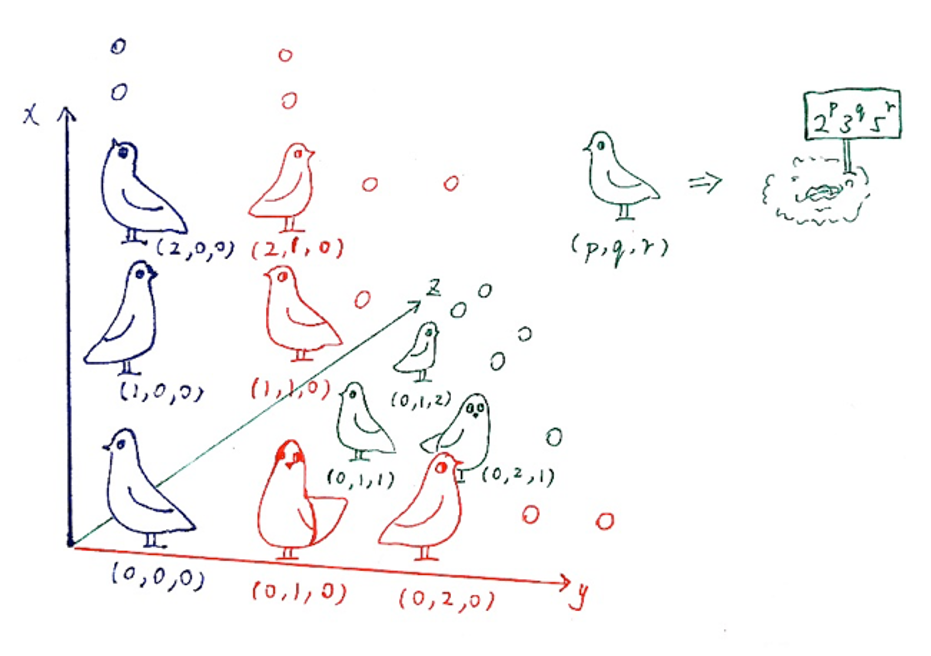
Zhaorui Xu: Sheltering Pigeons (and other thoughts on infinity)
Aditya Ghosh: Fermat’s Little Theorem

Aditya Ghosh: When do equations have solutions? (An introduction to Group Theory)
Aditya Ghosh: The Importance of being Symmetric

Aditya Ghosh: Modular Arithmetic and calculating expenses

Nanfan Yi: Infinite Wandering and Wondering
Nanfan Yi: Infinity – Go Wild or Go Home?

Nanfan Yi: Different Sizes of Infinities?!

Nanfan Yi: Infinity at First Glance (Perhaps a Stare)

Aarya Saraf: The Maths Behind Sex

Martha Bozic: What’s your type? The Maths behind the ‘Qwerty’ Keyboard

Joe Double: from aliens to bees via tattoos

Kai Laddiman: What are the chances that two England teammates share a Birthday?

Francesca Lovell-Read: Not so smooth criminals – how to use maths to catch a serial killer

Mariya Delyakova: Goldbach’s Conjecture – easy but hard
Kai Laddiman: Complex Numbers – they don’t have to be complex!

Joe Double: Maths proves that maths isn’t boring

Kai Laddiman: Spring into action and get ahead of the competition

Joe Double: Alien maths – we’re counting on it

Kai Laddiman: This robot is a ‘Cheetah’



